Title Text:After decades of studying the curve and the procedure that generates it, the consensus explanation is “it’s just like that.”
Origin:https://xkcd.com/2529/
https://www.explainxkcd.com/wiki/index.php/2529:_Unsolved_Math_Problems
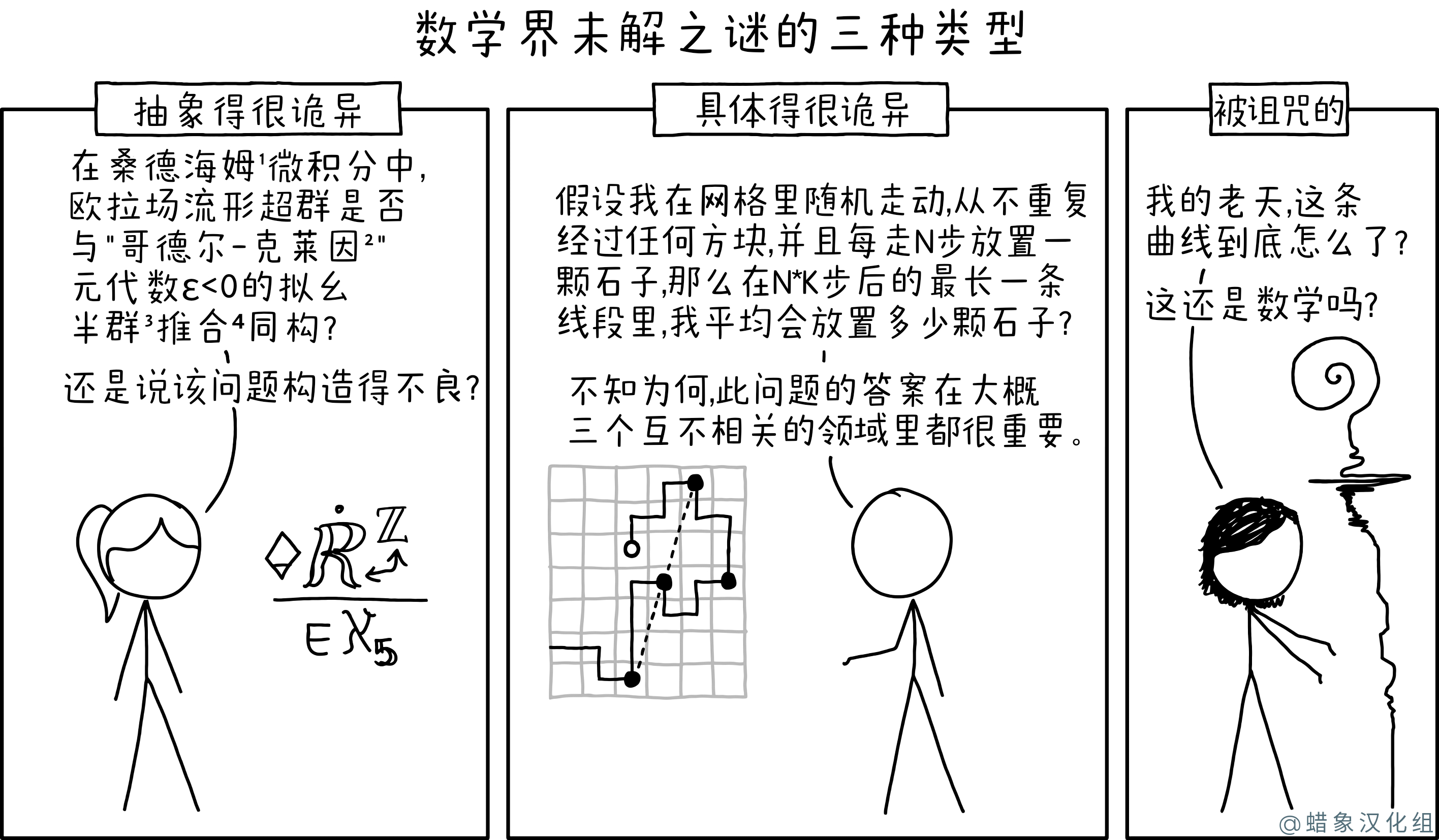
尚未解决的数学问题
注释:
1. 桑德海姆(Stephen Joshua Sondheim)是美国著名音乐剧及电影音乐作曲家及剧作家。他曾被评价“唱他的歌就好比歌手和演员需要学习微积分“。
2. 哥德尔(Kurt Friedrich Gödel),出生于奥匈帝国的数学家、逻辑学家和哲学家。克莱因(Felix Klein),德国数学家。两位数学家从未合作过。
3. 原文为quasimonoid,为虚构词汇,由quasi[group](拟[群])和monoid(幺半群)组合而成。
4. 原文为conjection,为虚构词汇,可能由conjecture(推测)和conjunction(结合)组合而成。
http://xkcd.in/comic?lg=cn&id=2529
数学有许多“未解决”的问题。这不仅仅是在等号两边找到正确数字的问题,而且通常需要证明或找到某些猜想的反例,或解释某些数学对象的某些性质。有时,这可能涉及将现有证明扩展到更广泛的数字,如实数、复数或矩阵。
一个具体的问题是一个与现实世界的过程有着非常明显的联系的问题,而一个抽象的问题是一个似乎与实际问题没有联系的问题。在现代数学中,许多问题往往非常抽象,首先需要复杂的符号来充分说明问题,就像许多千年问题一样。另一方面,许多未解决的问题非常具体;例如,有很多与将对象打包到空间相关的问题,虽然很容易陈述,但很难解决,例如Collatz 猜想。最后,兰德尔描述了第三类“被诅咒的问题”,它们具有奇怪的、看似随机的行为,例如湍流行为或素数分布。
在第一个面板中,马尾辫描述了一个奇怪的抽象问题。她的描述似乎是,要么数学或只是术语的无意义的混乱声数学。数学术语来自数学的不同分支:群论、拓扑学和微积分。
- 欧拉场:
- 歧管:
- 超群:
- 同构: 同构描述了一个结构的所有属性是否可以映射到另一个结构的属性。结构通常必须是相同的类型;目前尚不清楚超群如何映射到“猜想”。
- Gödel-Klein: Kurt Gödel是 20 世纪的数学家,研究逻辑和哲学(他最著名的是哥德尔不完备定理),而Felix Klein是 19 世纪的数学家,研究群论和几何;两人可能从未合作过。
- 元代数:
- ϵ<0:一个关于在分析中如何将ϵ定义为任意小的正数的笑话。
- quasimonoid:甲malamanteau,结合前缀“准”(意为“部分”或“似乎”)和“幺”(一种来自组理论对象),并且可能是指唤起字符卡西莫从巴黎圣母院(尽管quasimonoids 是一种代数对象,即非关联幺半群)
- 桑德海姆演算:这是指斯蒂芬·桑德海姆,美国音乐剧最成功的作曲家和作词家之一——他的音乐剧《走进森林》的制作人曾说过“唱歌斯蒂芬·桑德海姆就像歌手和演员的演算”。
- 猜想:这可能是猜想和合取的结合,也可能是正反加投影的笑话。
最后她问问题陈述是否格式错误;考虑到它主要是胡言乱语,这可能是真的。
许多真正未解决的数学问题看起来同样抽象。一个例子是霍奇猜想,一个千禧年奖问题。它指出“让 X 是一个非奇异复数射影流形。那么 X 上的每个 Hodge 类都是与 X 的复数子变体的上同调类的有理系数的线性组合。” 这些话在外行人看来可能是荒谬的。甚至对专家来说,这个问题也是“抽象的”。(给定一个特定的流形,即使是一个阿贝尔四重,你究竟如何确定给定的 2,2 类是否是一个循环?)
在第二个面板中,Cueball 描述了一个具体的随机游走问题,然后提到这在三个不相关的领域有应用。这其实并不少见。维基百科的文章说,“随机游走在工程学和许多科学领域都有应用,包括生态学、心理学、计算机科学、物理学、化学、生物学、经济学和社会学。在网格上随机行走,从不两次访问任何方块被称为自我-避免步行.” 这个小组的灵感可能来自一些关于自回避行走的棘手的未解决问题。其中许多问题与严格证明物理直觉猜测的随机行走的性质有关,因此这些问题与物理学有关. 关于一条线上的最大点数的部分让人想起组合几何中的问题,这通常涉及计算位于不同线上的点。模拟这种情况的Python代码可以在这里找到:[1]。
在最后一个面板中,梅根看到了一条似乎没有一致模式的奇怪曲线。在底部,它大部分是直的,有一些小摆动。在中间,它看起来像一个狂野的高频波,突然爆发然后消失。并且顶部是一个螺旋状的,看起来像一个问号或西式十字形。她想知道这是否甚至可以是数学的。一方面,考虑到绘制一些数学过程(例如Mandelbrot 集)所产生的奇怪形状,它很可能是。例如,未解决的黎曼假设,另一个千年奖问题,涉及奇怪且乍一看的随机曲线的特性。在数论中,术语“诅咒曲线”已被用来描述第13 级的“分裂 Cartan”模曲线,该曲线多年来一直拒绝尝试计算其有理点集。另一方面,是否可以是数学的问题表明这可能确实不是数学符号。曲线看起来像 unalome 符号,这是一个佛教符号,代表人生的道路,或启蒙之旅。可以说这确实代表了一个未解决的问题,尽管不是数学问题——这可能是幽默意义的一部分。
在标题文本中,最终面板中的曲线是根据研究它的小组的共识和生成它的程序进一步解释的,评论说“就像那样”作为他们的结论,这真的不是完全解释。