Title Text:The hard part about opening a hole in the proof of the Poincar茅 conjecture is that Grigori Perelman will come out of retirement to try to fix it by drawing a loop around the hole and contracting it to a point.
Origin:https://xkcd.com/2320/
https://www.explainxkcd.com/wiki/index.php/2320:_Millennium_Problems
千禧年难题
脚注:
[1]千禧年大奖难题(Millennium Prize Problems): 又称世界七大数学难题, 是七个由美国克雷数学研究所(Clay Mathematics Institute,CMI) 于2000年5月24日公布的数学猜想。
[2]同胚:如果两个空间之间存在同胚,从拓扑学的观点来看,两个空间是相同的。拓扑空间是一个几何物体,同胚就是把物体连续延展和弯曲,使其成为一个新的物体。因此,正方形和圆是同胚的,但球面和环面就不是。
[3]庞加莱猜想:其中三维的情形被俄罗斯数学家格里戈里·佩雷尔曼于2003年左右证明。2006年,数学界最终确认佩雷尔曼的证明解决了庞加莱猜想。在一个有边界的三维空间中,单连通就是这个空间中每条封闭的曲线都可以连续地收缩成一点,或者说在一个封闭的三维空间,假如每条封闭的曲线都能收缩成一点,这个空间就一定是一个三维球面。
http://xkcd.in/comic?lg=cn&id=2320
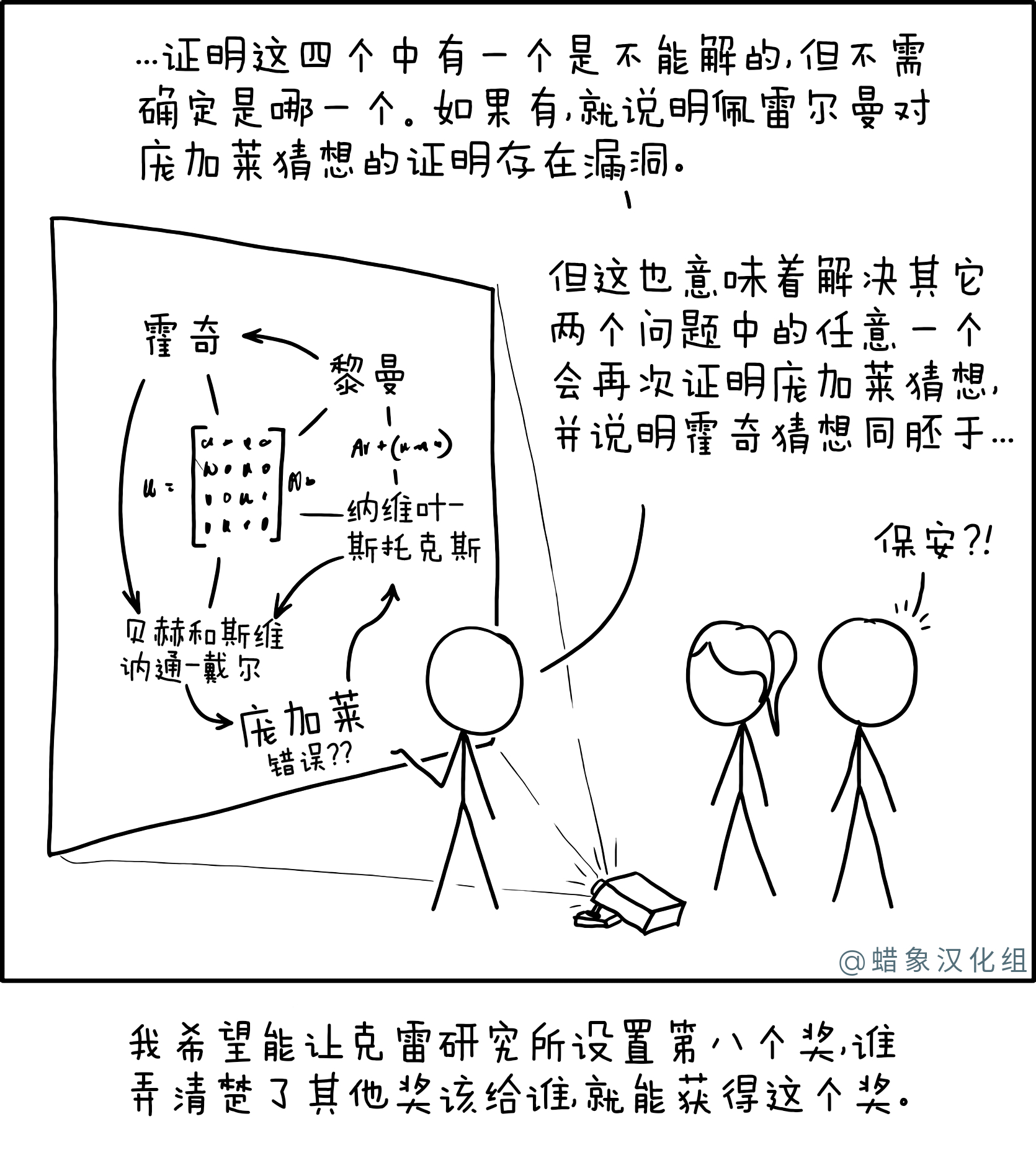
兰德尔(Randall)被称为Cueball,他正在展示关于千年奖问题的幻灯片,这是克莱数学学院在2000年指定为数学中最重要的未解决问题中的七个问题,是大卫·希尔伯特(David Hilbert)列出的23个问题中的一种于1900年发布。七个问题是:
- 的P对NP问题,无论是否有问题的解决方案,其可以在多项式时间来验证这个问题必须一定具有用于产生在多项式时间中的溶液的方法。认为不是这种情况,即“ P!= NP”,但尚未得到证明(在Cueball的幻灯片中也未提及)。
- 代数几何中的霍奇猜想。
- 庞加莱猜想(Poincaréconjecture)断言3球(4维球的“表面”)是唯一闭合且简单连接(即无孔)的3维空间。它是由Grigori Perelman于2003年解决的,是迄今为止解决的七个问题中的唯一一个。
- 在黎曼假设,其中声称,所有非平凡零点黎曼ζ函数具有实部分的二分之一。
- 在杨-米尔斯的存在和质量的差距,为什么色力由胶子无质量传送,但只有在大量的颗粒观察到的问题。Cueball的幻灯片上未提及这一内容。
- 的纳维-斯托克斯存在性与光滑性的问题,这问题是否存在必须对溶液Navier-Stokes方程(流体运动定律),用于任何光滑组初始条件。
- 该桦木和斯维讷代尔猜想,缩写为“白桦/ SD”在这里,它声称,有一个简单的方法来告诉Rational解决方案的数量的椭圆曲线。
尽管证明庞加莱猜想的数学家格里戈里·佩雷尔曼(Grigori Perelman)拒绝了他的奖金,但每个问题都有100万美元的奖金。
兰德尔(Randall)试图证明各种问题之间的关系。根据演示文稿,证明一个人可能会反证或证明其他人,并且问题之间的拟议互动是如此复杂,以至于研究所可能决定向任何能够找出任何给定证据确实解决了一个或多个问题的人授予额外的奖励。 。这八奖可能由佩雷尔曼拒绝的奖项资助。
兰德尔以前因各种挑衅行为而被禁止参加会议;大概他也正要被赶出克莱数学研究所,因为“另一个” Cueball已经在呼吁安全。但是,这似乎只是这三个人,因此这一次不应该禁止会议。
标题文字提到,如果有人在Perelman的庞加莱猜想证明中发现一个漏洞(缺陷或错误的常见表达),这位着名的隐居作者可能会再次出现并通过应用微分的理论数学来解决问题。在逻辑结论序列中,与“孔”相比,“孔”具有不同含义的几何形状。所建议的将孔封闭成环然后缩小的方法使人想起了Perelman解决庞加莱猜想的特定技术(带手术的Ricci流)。