Title Text:I mean, if it’s that easy to get a theorem named for you … “a straight line that passes through the center of a coplanar circle always divides the circle into two equal halves.” Can I have that one? Wait, can I auction off the naming rights? It can be the Red Bull Theorem or the Quicken Loans Theorem, depending who wants it more.

Origin:https://xkcd.com/2042/

https://www.explainxkcd.com/wiki/index.php/2042:_Rolle%27s_Theorem

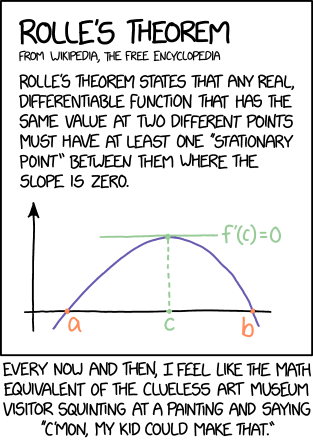
在数学中，可微函数是一种在任何地方都是“平滑”的函数，没有任何突然的中断或尖的“扭结”或类似的东西。这种函数的导数是表示原始函数的“斜率”或“变化率”的新函数。此漫画中的功能从点（a）向上（c）上方的点向上弯曲，平滑地转动，然后从（c）向下弯曲到（b）。结果，该函数的导数从（a）到（c）是正的，然后从（c）到（b）是负的。在（c）本身，函数是“平坦的”：放大的越多，它看起来越横向。该函数既不向上也不向下移动，因此导数既不是正数也不是负数，而是零。这就是f’（c）= 0意味着，因为f’是微分计算中函数f的导数的通用符号。

数学中的一个定理是一种陈述，它已经从以前被接受的陈述中得到证明，就像其他定理或公理一样。这部漫画引用了罗尔的定理。该定理基本上表明，如果平滑变化的函数在两个不同的输入处具有相同的输出，则它必须在其间具有一个或多个转折点，因为在每个输出处导数为零。作为一种特殊情况，如果两个输入之间的函数保持平坦，那么对于输入之间的每个点，其导数实际上为零。对Randall来说，这是显而易见的。然而，这个定理的证明并不像结果那么明显。

这个定理似乎微不足道，再加上赋予定理名称的荣誉，导致兰德尔与艺术博物馆的参与者进行比较，他们看到抽象艺术作品，并且只看到作品中明显的技术简洁性。这样的访客可能会惊呼“我的孩子可以画出那个！”。然而，这种艺术品通常被视为具有除了实现该作品的绘画难度之外的属性的价值。例如，艺术家在这种风格中的作品可能因其有远见的品质或通过选择颜色或纹理而表达的情感而受到称赞。其中一位艺术家是杰克逊波洛克。 “无能”的访客没有看到这些方面，并认为他们的孩子可以模仿这件作品。兰德尔建议他在看到罗尔定理时会有类似的感受，并且只注意到明显的正确性，而不承认证明的复杂性或定理的其他隐藏方面。

在标题文本中，Randall提到了一条线和一个共面圆。这仅仅意味着这些二维物体必须位于更高，三维或更多维空间中的同一平面中。通过这种方式，通过圆心绘制的每条直线只是一个直径，将它分成两个相等的部分。即使这个事实是微不足道的，Proclus说第一个证明它的人是Thales。在标题文本中还注明了命名权的拍卖，是指为支付特权的公司命名娱乐场所的做法，例如三个红牛竞技场或快速贷款竞技场中的任何一个。此外，“Rolle’s”听起来像“Rolls”，这是Rolls Royce品牌的常见缩写，意味着可能由英国汽车制造商赞助。数学定理的命名（以及引理，方程，定律，方法等）并不总是直截了当的，往往会导致误导性的名称。

兰德尔暗示有许多看似简单的定理。例如，Dirichlet的盒子原理，也称为Pigeonhole原则，指出如果你有更多的对象而不是容器，你将不得不在一个容器中放置至少两个对象。