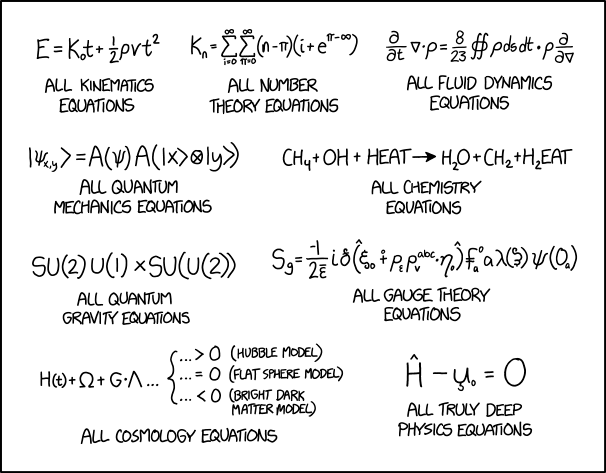Title Text:All electromagnetic equations: The same as all fluid dynamics equations, but with the 8 and 23 replaced with the permittivity and permeability of free space, respectively.

Origin:https://xkcd.com/2034/

https://www.explainxkcd.com/wiki/index.php/2034:_Equations

这部漫画给出了一组模拟方程式。对于那些不熟悉该领域的人来说，他们看起来与你在研究论文或相关维基百科页面上看到的非常相似。大多数笑话与给定字段中大多数方程的符号或“外观”有关。

漫画制作了关于运动学，数论，流体动力学，量子力学，化学，量子引力，规范理论，宇宙学和物理方程等领域的笑话。当然，列出的所有方程式都不是真正的方程式（H2EAT显然是笑话并且是对给定字段的嘲弄）。和往常一样，兰德尔只是在笑。

所有运动学方程

大多数运动学方程式倾向于大量使用常数，加法，幂和乘法。该特定方程类似于实际运动学方程d = vt + 1 /2at ^ 2，但用v（速度）时间（密度）代替（加速度）并用“K0”代替速度，“K0”不是运动学中使用的术语。

所有数论方程

兰德尔开玩笑说数论如何经常涉及使用求和。在双重求和中使用π作为整数变量是一个笑话，因为π基本上总是用于众所周知的常数3.14159 ……，而不是变量。使用i作为求和变量是常见的，尽管它也可以与假想单位√-1混淆。常数e，i和π以及理论上界通常出现在数论方程中。

所有流体动力学方程

流体动力学方程通常涉及大量积分，特别是那些在这里所做的封闭轮廓上的积分，这通常是这些方程式对外人的主要说明因素。时间导数和梯度算子在流体动力学中很常见，主要是通过Navier-Stokes方程，流体密度是中心重要性的函数之一。 8/23分数是一个奇怪的选择，但在流体动力学中会出现各种意想不到的分数。 ds和dt采用双轮廓积分（s可能是距离，t是时间），但是非常不允许相对于末尾的导数。

所有量子力学方程

量子力学通常涉及列出的一些外观符号，包括bra-ket符号，张量积和量子态的希腊字母Psi。具体来说，等式的左边是标记为Psi的ket状态，它取决于x和y（可能是位置），而右边可能是依赖于状态Psi的运算符A（具有这样的状态非常罕见）依赖）作用于看起来像该运算符的另一个副本，它取决于由x和y标记的状态的外部产品（再次奇怪）。慈善解释可能是第二个A是算子A的本征函数A.通常，这通过给操作符给出“渉”（^符号）或使本征函数成为本征态来清楚地表明，但是由于等式故意胡说八道A’是模棱两可的。另请注意，这里的bra-ket数学不一致，因为左边是一个ket，但是右边只有两个A’，它们既是运算符，也是函数，但绝对不是kets。

所有化学方程式

化学方程使用化学化合物的公式来描述化学反应。如图所示，这些等式显示左侧的起始化学物质和右侧的所得产物。有时，这样的等式可以任选地指示需要激活能量，以使反应在合理的时间范围内发生，例如，通过加热。需要加热的反应通常用希腊大写字母Delta（Δ）或反应箭头上方的指定温度表示，但该漫画使用左侧的“+ HEAT”术语代替。笑话是Randall将“HEAT”解释为另一种化学物质，它与氢气（H）反应成H2EAT，这是无意义的，因为热量在这里传递能量，而不是添加物质。无论如何，兰德尔得到的这个方程的化学计量是正确的，在方程的每一边都有相同数量的所有类型的“原子”。

所有量子引力方程

量子引力使用由大写字母表示的数学组，如图所示。 SU（2），U（1）和U（2）都是经过充分研究的群体，尽管’SU（U（2））’没有意义。缺乏关联者意味着这种表达不是一个等式。这是一个可能的双关语，在“苏你也……你赢了”……“你也是，你也是”，虽然现在还不清楚它是如何适应这里的。

Sg =（ – 1）/（2ε＆＃x304;）ið（＆＃x302;ξ0＆＃x2a22;p∈ρvabc⋅η0）＆＃x302; f＆＃x335;a0λ（ξ）ψ（0a）

所有规范理论方程

量表理论是场论的一个子集。大多数规范理论方程看起来都有许多奇怪的常数和带有奇数标签的变量。

所有宇宙学方程宇宙学是宇宙发展和最终命运的科学。这里的笑话可能与宇宙学领域中接受的不同模型有关。 H是哈勃参数，Ω是通用密度参数，G是引力常数，Λ是宇宙常数。

＆＃X124; – 你＆＃x327; 0 = 0

所有真正深刻的物理方程

关于“真正的深度物理方程”的笑话是，大多数通用物理方程都很简单，几乎非常如此。一个例子是爱因斯坦的E = mc虏。

标题文本引用了这样一个事实：电场和磁场经常用物理学生用流体动力学的类比来解释，以及它们确实有一些相似之处（仅在数学描述方面称为三维矢量场） ）用流体。介电常数常数（用ε0表示）和磁导率常数（用μ0表示）是与在真空中产生特定量的电通量所需的电荷量和真空支持磁场形成的能力相关的系数，分别。它们经常出现在麦克斯韦方程（定义经典力学中的电场和磁场的方程式）中，所以兰德尔正在开玩笑说，任何与它们在一起的表面都是自动的电磁学方程式。