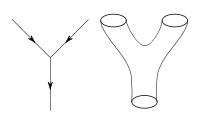
Title Text:Theoretical physicist: At the Planck length, uncountably many.
Origin:https://xkcd.com/2658/
https://www.explainxkcd.com/wiki/index.php/2658:_Coffee_Cup_Holes
咖啡杯的洞

http://xkcd.in/comic?lg=cn&id=2658
这部漫画描绘了不同研究领域的人回答“咖啡杯上有多少个孔?”的问题。并将其与正常人会说的话进行比较。
这个问题有不同的解释,完全取决于洞的定义。漫画中展示的这种咖啡杯是带把手的(像马克杯),但兰德尔称它为杯子,在咖啡杯的维基百科页面上也有带把手的杯子。大多数人会认识到手柄上有一个孔。
漫画通过几个人的思路来探寻问题的答案,因含糊而搞笑:
拓扑学家[编辑]
拓扑学家Ponytail指出咖啡杯属于单孔类。从拓扑学家的角度来看,咖啡杯肯定有一个孔,对应于杯柄形成的开口。没有把手的杯子是零孔,因为它相当于一个餐盘,只是表面有一个凹痕。有关拓扑的更多信息, 请参阅2625:场拓扑。
整个小组引用了一个学术笑话,其中拓扑学家无法区分带把手的咖啡杯和甜甜圈,因为它们彼此同胚——这意味着它们具有相同的属(即一个孔)。
正常人[编辑]
毛毛代表正常人,不确定(缩写“IDK”代表“我不知道”),并要求澄清顶部的开口是否算作一个洞。这显示了问题中的缺陷,该问题受到“孔”一词在数学上不精确、模棱两可的常见用法的影响。拓扑学家将开口称为凹面,而不是孔,虽然他们通常在他们的领域之外考虑这种几何特性,但拓扑的大多数实际应用确实涉及几何组件。相比之下,在日常使用中,许多凹面被称为孔洞,例如用铲子在泥土中挖出的孔洞。Hairy 会说手柄是一个,如果开口算作一个洞,他会说两个,他不确定问这个问题的人是怎么想的。
哲学家[编辑]
发髻,一位哲学家,考虑到一个假设的场景,用一个阐明性的反问题来回答这个问题。人们可能会期望钻一个新孔也会将孔的数量增加一个。但是,如图所示,有些人会认为新的安排有三个孔(除了手柄,顶部有一个可以倒咖啡的孔,底部有一个可以倒咖啡的孔),而其他人会认为它只有两个(新孔与顶部的原始开口形成一个连续的孔,咖啡可以从中流出)。事实上,有些人可能会说咖啡杯现在有一个孔是因为它漏水了,忽略此时的手柄拓扑。通过这种方式,她要求对话者直面歧义,并思考“洞”这个词在不同语境中的含义。
化学家[编辑]
化学家Cueball在分子水平上观察杯子中的咖啡。他设想了咖啡中咖啡因分子的球棒模型,并估计了所有咖啡分子的孔总数。他得出了一个真正庞大的数字: “仅咖啡因”就有 1,000,000,000,000,000,000,000(10· 21或 1 六十亿)。一分子咖啡因有两个带孔的键环,乘以 500 quintillion 分子,或 0.00083摩尔。由于咖啡因的分子质量约为每摩尔 194 克,Randall必须认为一杯典型的咖啡中咖啡因的质量是 161 毫克。咖啡可能有其他孔,具体取决于咖啡的类型;例如,浓缩咖啡含有大量的烟酸和核黄素,它们的化学结构分别有一个环和三个环。
这种估计取决于从字面上理解分子的球棒模型。然而,真正的分子键不是固体棒,而是原子之间共享的电子云。分子环中间的“空穴”并不完全是空的,而只是通过中间的电子概率密度低于键的其他部分。因此,电子轨道和键的点云二元性可能无法满足拓扑学家、普通人或哲学家对可能形成孔洞的连接基板的标准。
理论物理学家[编辑]
在标题文本中,一位理论物理学家在普朗克单位的亚原子尺度上看得更深。由于基本粒子相互作用受基本力和碰撞(根据泡利不相容原理)而不是拉伸或延展性固体连通性支配,理论物理学家假设任何提供单个孔的定义也将描述许多孔,类似于阶乘宇宙中粒子的数量,[1]或至少在杯子的光锥内,这是一个无法准确计算的数字,但在数学意义上并非不可数。
实际考虑[编辑]
主要的笑话是,洞的数量取决于你看待世界的规模和视角。从拓扑学的角度来看,当有人挖到地下时,它应该一直穿过(或者更容易,在另一个地方再次上下),然后才被认为是一个洞,因为洞是其他东西应该能够通过的东西通过。但从一般用法的角度来看,如果人们在地下挖洞,结果称为洞,因为从功能上讲,它会造成不连续性,例如,可以在其中放置或掉落东西。同样,没有把手的咖啡杯或一瓶啤酒的开口称为孔,尽管它们在拓扑上等同于餐盘,正常人永远不会说有孔。
表面中的空腔也可以被视为物理屏障,防止在某些情况下沿表面移动(例如下水坑在道路中间打开),尽管它在拓扑上可能以最一般的方式是“平坦的”,因此对上下文非常开放,并且这样的孔可能被认为比表面更像一个“东西”移除以创建它。并且可以容纳液体的容器中的凹面(或去除这种能力的钻孔)与作为其中液体一部分的分子中的孔具有不同的性质。这些洞与普朗克尺度的弦理论洞非常不同,后者不一定涉及障碍、包容或拓扑连通性的任何其他方面。这种孔是什么或意味着什么的概念上的模糊性由虚构的便携式孔证明,它服从和违抗正常人’
这里关于杯子和甜甜圈的拓扑讨论与人身上有多少个洞的问题有关,Vsauce 的视频 How Many Holes Does a Human Have?中很好地回答了这个问题。. 这也很好地了解了纸杯和带把手的马克杯之间的拓扑差异,以及一个如何变成盘子而另一个变成甜甜圈。