Title Text:G枚del should do an article on which branches of math have the lowest average theorem number.
Origin:https://xkcd.com/2610/
https://www.explainxkcd.com/wiki/index.php/2610:_Assigning_Numbers
分配数字

注释:
哥德尔不完备定理:在数理逻辑中,哥德尔不完备定理是库尔特·哥德尔于1931年证明并发表的两条定理。简单地说,第一条定理指出:任何自洽的形式系统,只要蕴涵皮亚诺算术公理,就可以在其中构造在体系中不能被证明的真命题,因此通过推理演绎不能得到所有真命题(即体系是不完备的)。
这是形式逻辑中的定理,容易被错误表述。有许多命题听起来很像是哥德尔不完备定理,但事实上并不是。具体实例见对哥德尔定理的误解。
把第一条定理的证明过程在体系内部形式化后,哥德尔证明了第二条定理。该定理指出:任何逻辑自洽的形式系统,只要蕴涵皮亚诺算术公理,它就不能用于证明其本身的自洽性。
哥德尔不完备定理破坏了希尔伯特计划的哲学企图。大卫·希尔伯特提出,像实分析那样较为复杂的体系的兼容性,可以用较为简单的体系中的手段来证明。最终,全部数学的兼容性都可以归结为基本算术的兼容性。但哥德尔的第二条定理证明了基本算术的兼容性不能在自身内部证明,因此当然就不能用来证明比它更强的系统的兼容性了。
哥德尔编号:在形式数论中,哥德尔编号是对某些形式语言的每个符号和公式指派一个叫做哥德尔数(GN)的唯一的自然数的函数。这个概念是哥德尔为证明他的哥德尔不完备定理而引入的。
http://xkcd.in/comic?lg=cn&id=2610
这种解释在数学上是不完整或不正确的。
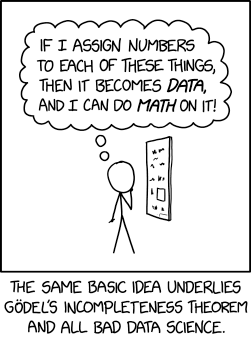
Cueball正在落入一个常见的陷阱,因为一点点知识是一件危险的事情。面对某种未知类型但似乎本质上不是数学性质的信息,他决定一种可能的方法是将所有内容转换为可以组合和数字比较的值。
在计算语言学或运动分析等不同领域,这是一件非常常见的事情,并且可以成为理解和学习有关主题的新事物的强大工具,因为数据科学试图从潜在的嘈杂和无序的事实中提取知识和见解. 但它也被用来通过使用关于如何表示源材料的不正确或错误的想法来实施糟糕的科学。虽然可以随意地将数值分配给随机数据,但这些数字通常没有足够的意义来计算并从中得出任何有用的推论。通常只能对实际测量值进行统计分析,而不是对可能有效地任意分配的值进行统计分析。
数据科学家常用的机器学习算法通常要求其所有输入都是数字的。然而,大多数数据集都包含分类特征(例如,一件家具的描述:椅子、桌子……)。因此,数据科学家使用编码技术将这些分类特征转换为数字形式,以便它们可以用作机器学习模型的输入。例如,标签编码包括将一个整数任意分配给一个类别(椅子=0,桌子=1,…),这对大多数观察者来说可能看起来毫无意义。在各种情况下,他们可能是对的。
因此,它不仅是 20 世纪数学中最深刻的定理之一的基础,它还可能被误用于各种糟糕或被误导的科学。从 Cueball 的态度来看,他的尝试能否可靠地将他的项目转化为数值系统,也不清楚他是否试图“在上面做数学!” 将更有能力。
研究这个概念的主要人物之一是库尔特·哥德尔。他用他标志性的不完备性定理介绍了哥德尔编号的概念。其中,每个公理、陈述和证明都分配了一个唯一的自然数,否则可能很难在任何其他类型的方法中准确处理。相反,现在可以用数学语言创建元数学语句。
这使得哥德尔能够以数学上严格的方式做出“这个陈述不能基于所提供的公理来证明”的陈述。一个简单的矛盾证明表明该陈述不能为假,因此(在大多数逻辑系统中)必须为真。证明如下: 1. 假设“不能从公理证明此陈述”(称此陈述 G)为假。[1] 2.因此可以从公理证明G。[2] 3. 公理存在。[3] 4. 因此,G 为真。[4] 5. 因此,G 也不是 G。[5] 6. 这是一个矛盾,因此 A(即“非 G”)或 B(ZFC)一定是错误的。我们不愿意牺牲假设 B,所以我们必须得出结论,在给定 B 的情况下 A 是错误的。[6] 7. 因此,G.
以上内容的解释性脚注[编辑]
- Jump up↑ 将此假设称为 A。
- Jump up↑ 因为否定的否定是肯定的。仅基于 A。
- Jump up↑ 将此假设称为 B
- Jump up↑ 通过Modus ponens应用于 2 和 3,基于 A 和 B
- Jump up↑ via Conjunction Introduction应用于1和4,基于A和B
- Jump up↑ 荒谬的归约适用于 1,3 和 5
请注意,哥德尔陈述的真实性不依赖于任何特定的公理集,并且添加公理(例如“哥德尔的特定陈述为真”)只会打开无法基于扩展的公理集证明的陈述的新迭代(诸如“与哥德尔的特定陈述具有相似性质的所有陈述”这样的陈述不足以作为公理。)。因此,通过更多的工作,可以证明任何足够健壮以适应算术的逻辑系统都必须包含在系统内为真但在系统内无法被证明或反驳的事实。这一结果的重要性不容小觑,因为它颠覆了整个数学哲学。 大卫希尔伯特著名的宣言“我们必须知道,我们会知道”是完全错误的。… 要么,要么(具有讽刺意味)哥德尔使用“不一致”或“不完整”的系统来产生他的结果。
标题文本建议哥德尔应该通过计算所有领域定理的哥德尔数的平均值来对不同的数学分支进行这样的分析。这是荒谬的,原因有很多:
- 1)哥德尔早就死了,死人不能写文章;[可疑] – 见599:天启
- 2)哥德尔数增长非常快,并且很大程度上取决于分配给每个逻辑运算符的特定值。因此,可以简单地通过更改每个运算符的编号顺序来操纵结果;
- 3)可能很难收集一个领域的所有定理,甚至是一个有代表性的样本;
- 4) 不同的科学领域,如生物学或人类行为,可能无法用哥德尔不完备定理的数学语言写出他们的定理
如果有人尝试这种形式的分析,那将是标题中描述的糟糕数据科学的一个例子。