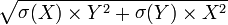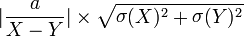Title Text:’Garbage In, Garbage Out’ should not be taken to imply any sort of conservation law limiting the amount of garbage produced.
Origin:https://xkcd.com/2295/
https://www.explainxkcd.com/wiki/index.php/2295:_Garbage_Math
无用数学

脚注:
[1]在计算机界有GIGO原则,意为:往计算机输入一堆垃圾,输出的一定也是一堆垃圾数据。
http://xkcd.in/comic?lg=cn&id=2295
这部漫画用数学表达式说明了“ 垃圾进,垃圾出 ”的概念。它显示了,如果您将垃圾作为计算的输入,那么结果很可能会得到垃圾,除非您乘以零,这消除了结果的所有不确定性。
口语中描述了算术,其他数学运算和统计信息中的错误传播。精度较低的数字称为垃圾,而精度较高的数字称为精确。下表按照方差来量化从操作数到结果的精度变化,用方差 σ(等于标准偏差的希腊小写字母sigma)或方差的平方根表示。方差或标准偏差是不确定性的常见规范(例如,作为公差区间的替代方法)。
数学运算的准确性和精确度对应于不确定性的传播规则,其中“垃圾”数将对应于具有高度不确定性的估计,而精确数则具有较低的不确定性。此类操作结果的不确定性通常对应于不确定性最高的术语。用于计算算术平均值的关于N条独立垃圾的规则反映了中心极限定理如何预测,当对独立估计值求平均时,估计值的不确定性(或标准误)将减少。
| 公式如图所示 | 导致不确定性 | 说明 |
|---|---|---|
| 精确数字+精确数字=精确度稍差 | 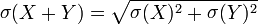 |
如果我们知道绝对误差线,那么加两个精确的数字将最坏地增加两个误差线的大小。例如,如果我们的精确数字是1(±10 -6)和1(±10 -6),那么我们的总和就是2(±2·10 -6)。如果结果总和由于将近似值加一个数字而接近零,则可能会损失很多相对精度,这种现象称为灾难性抵消。因此,两个数字都必须为正,以使所声明的说法正确。 |
| 精确数字×精确数字=精确度稍差 | 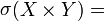
|
在这里,代替绝对误差,将添加相对误差。例如,如果我们的精确数是1(±10 -6)和1(±10 -6),那么我们的乘积就是1(±2·10 -6)。 |
| 精确数字+垃圾=垃圾 | 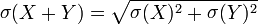 |
如果这些数字之一具有很高的绝对误差,并且所添加的数字具有可比较的大小,则此误差将传播到总和。 |
| 精确数×垃圾=垃圾 | 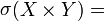
|
同样,如果其中一个数字具有较高的相对误差,则此误差将传播到产品中。在此,这与数字的大小无关。 |
| √ 垃圾 =少垃圾 | 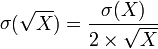 |
计算数字的平方根时,其相对误差将减半。取决于应用程序,这可能并没有那么好,但至少还没有那么糟糕。 |
| 垃圾2 =更糟的垃圾 | 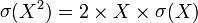 |
同样,当数字平方时,其相对误差也会加倍。这是乘法增加相对误差的必然结果。 |
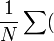 N个统计上独立的垃圾 N个统计上独立的垃圾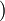 =更好的垃圾 =更好的垃圾 |
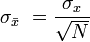 |
通过汇总许多统计上独立的观察值(例如,调查许多个人),可以将相对误差减少到平均值的标准误差。这是统计采样和中心极限定理的基础。 |
| 精确数量的垃圾 =更糟糕的垃圾 | 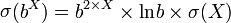 |
指数对变化非常敏感,它也可以根据精确数字的大小来放大影响。 |
| 垃圾–垃圾=更糟糕的垃圾 | 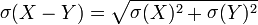 |
这条线涉及灾难性的取消。如果两部分垃圾大致相同(例如,如果它们的错误条重叠),则答案可能是肯定的,零或否定的。 |
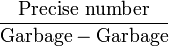 =更糟糕的垃圾,可能被零除 =更糟糕的垃圾,可能被零除 |
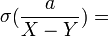
|
确实,和上面一样,如果误差线重叠,那么我们可能最终被零除。 |
| 垃圾×0 =精确数字 | 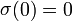 |
任何东西乘以0都会得出0,这是一个非常精确的数字,因为我们自己提供了0,因此它没有任何错误。这等效于从统计分析中丢弃垃圾数据。 |
标题文本是指计算机科学中的“垃圾填入,垃圾填入”的格言,其中指出,在涉及计算机代码时,即使代码本身准确地执行了应做的工作,提供错误的初始数据也会产生错误的结果。 。但是,正如我们在上面看到的,尽管有一些方法可以减少此错误(例如汇总数据),但是将数据插入数学公式时,这可能会放大我们输入数据的错误。因此,垃圾的数量不一定是保守的,而相比之下,其他科学一样数量的能量和动量总是守恒的。