Title Text:It’s the NORMAL distribution, not the TANGENT distribution.<
Origin:https://xkcd.com/2118/
https://www.explainxkcd.com/wiki/index.php/2118:_Normal_Distribution
常態分佈
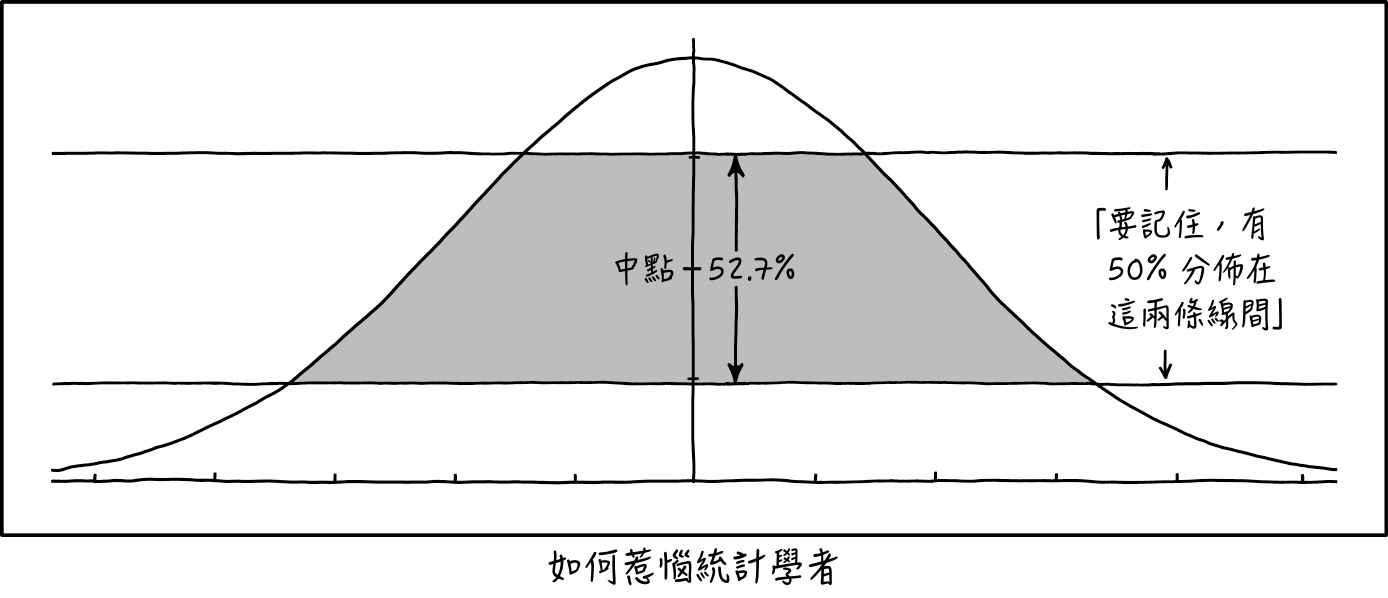
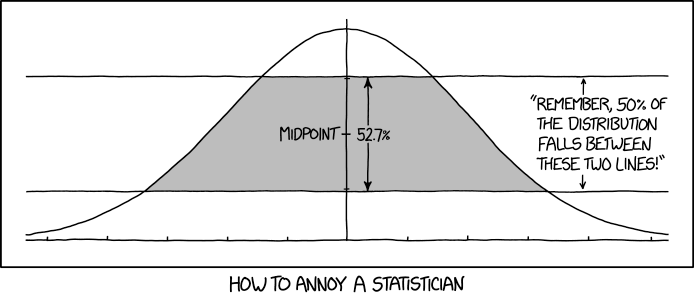
正态分布和标准差的间隔是介绍性统计中常见的主题。兰德尔的图表很相似,但他的线条是垂直的。
在统计学中,分布是一种表示,可以根据预期有多少样本落入离散区间或特定值范围之间来理解。例如,如果您想使用十年(0-9,10-19等)的箱子来表示年龄分布,您可以生成一个条形图,每个箱子有一个条形,其中每个条形的高度代表一个与该箱匹配的样本部分的计数。要将条形图转换为分布,你会得到无数的人(技术上:数字N倾向于无穷大),将它们放入无限窄的年龄箱(技术上:大小为O的箱(1 /sqrt( N))),然后将每个bin计数除以总计数,使整个事物加起来为1.通常要问两条垂直线之间的分布有多少;这相当于询问预计两个年龄段人口的百分比。
许多统计抽样类似于称为“正态分布”的模式。理论上完美的正态分布将具有无限的样本大小和无限小的区间。这将产生一个与漫画中曲线形状相匹配的条形图。
分布的两条垂直线之间的区域表示随机选择的X值在线的X值之间的概率。相反,Randall找到两条水平线之间的区域,这在数学上是无意义的,因为概率分布的Y轴通常用来表示幅度为单位的分数。在上述年龄分布类比中,具有相同X值的两个点可以理解为代表两个年龄相同的人;但是,就类比而言,不能轻易理解具有相同Y值的两个点。在任何给定水平位置由“大小”表示的项目是无法区分,无序和可互换的;两个物品碰巧落在Y轴上的同一位置这一事实并不意味着它们有任何共同之处。
简而言之,兰德尔发明了一种新的概率分布,标题文本幽默地暗示应该称之为正切分布。该分布定义如下:考虑漫画中曲线与水平轴之间的区域,并考虑在该区域中均匀分布的随机点(X,Y)。然后X具有正态分布,Y具有正切分布。漫画中垂直线之间的区域给出了关于X的概率,漫画中水平线之间的区域给出了关于Y的概率。漫画正确地指示如果我们让R是Y值的区间,即Y的中心范围的52.682%在该范围的中点处,任何随机选择的Y值具有落入区间R内的概率1/2。
以前从未讨论过这种分布,并且没有已知的应用。此外,Y的分布不对称:50%的Y值落在区间R内,41%落在R之下,只有9%落在R之上。因此漫画中的单条信息不是一个好的描述方式这个发行!我们确实使用这样的间隔进行正态分布,因为正态分布是对称的,对称中心是平均值,中值和模式。 (然而,观察到标准正态分布中50%的X值落在垂直线X = -0.2和X = 1.41之间,这几乎是荒谬的。)
标题文本指的是几何中法线和切线的概念。给定2D曲线或3D曲面,从曲线或曲面上的点垂直向外指向的线(与曲线成90度角)被认为是曲线的法线,而刚刚掠过曲线的线,与接触点处的曲线完全平行,据说与该点处的曲线相切。这种几何正常概念与统计正态分布完全无关。兰德尔观察到,如果你采用几何法线并将其旋转90度,则会产生切线;因此,如果采用正态分布并将其旋转90度,则必须得到称为“切线分布”的东西。对统计学家这样说只会让统计学家更加恼火。这对统计学家来说很烦人,不仅因为术语法线和切线来自微分几何,而且在概率论中没有确定的含义。即使是垂直这个词在概率论中也没有确定的含义。当然,漫画中的x和y坐标是垂直(正交)坐标,但X和Y不是“垂直”或“正交”随机变量。即使我们给出“垂直”或“正交”概率意义,并且最明显的这种意义要么是独立的,哪个甚至使用与几何符号相关的符号来表示垂直,或者不相关,这使得X和Y正交向量在Hbebert空间的随机变量是相对于Lebesgue测量的方形可积,X和Y在这两种意义上都不是垂直的。
所以你知道的概率和统计越多,这部漫画就越烦人。这不仅仅是混淆新手。