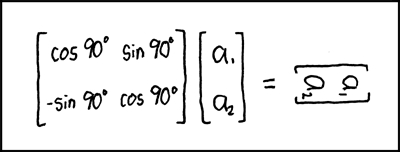Title Text:In fact, draw all your rotational matrices sideways. Your professors will love it! And then they’ll go home and shrink.

Origin:https://xkcd.com/184/

https://www.explainxkcd.com/wiki/index.php/184:_Matrix_Transform

矩阵变换

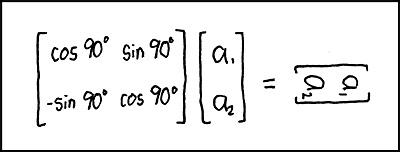
https://www.douban.com/photos/photo/827024692/

旋转矩阵变换（即，其中具有“cos”和“sin”的大括号）用于计算机图形中以旋转图像。通常，要在2D空间中顺时针旋转点[a1，a2]，可以将其乘以旋转矩阵[cos z°，sin z°; -sin z°，cos z°]。在这种情况下，等式的左侧旋转[a1，a2] 90°。简化三角法，90°顺时针旋转矩阵为[0,1; -1,0]，所以乘以[a1，a2]，你得到[a2，-a1]。

笑话是作者对矢量图像执行旋转变换而不仅仅是矢量本身。

旋转矩阵变换是一般线性矩阵变换的一种特殊情况，它可以对图像做其他事情，包括缩放它们或平移（移动）它们的其他两个仿射变换。在一个学究的笔记中，通常数学使用逆时针作为默认值，虽然计算机图形经常使用顺时针默认，所以这可能是一个有意的参考。

因此，标题文本可能指的是教授回家（翻译）和缩小（缩放）的笑话，也可能是指他们回家并看到他们对学生理解的绝望感到畏缩。