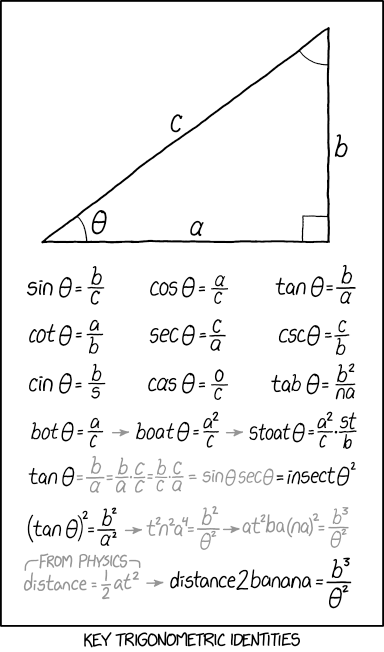
Title Text:ARCTANGENT THETA = ENCHANT AT TARGET<
Origin:https://xkcd.com/2070/
https://www.explainxkcd.com/wiki/index.php/2070:_Trig_Identities
三角恆等式
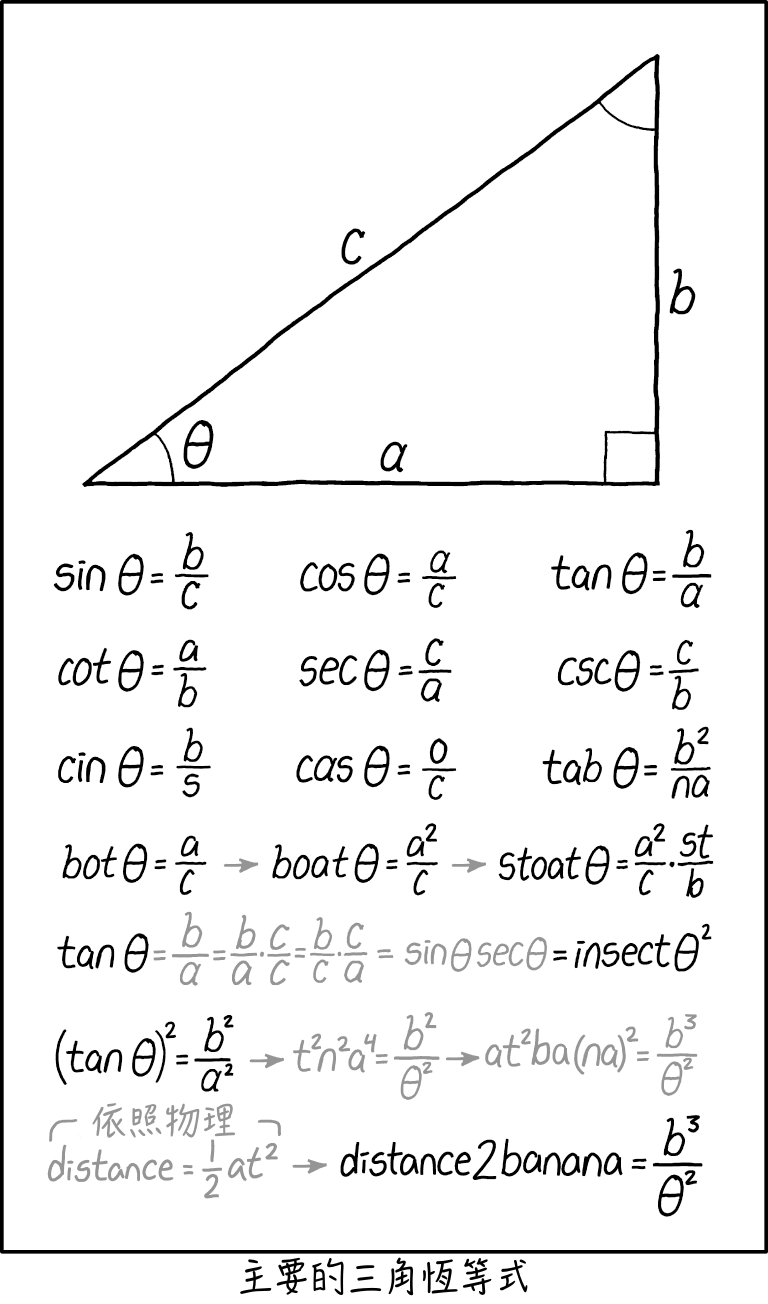
这个漫画在前两行显示了几个真正的三角恒等式,并且通过将代数方法应用于三角函数名称中的字母而进一步低于某些身份“派生”,这显然是无意义的。
第一行是已知的三角函数:正弦,余弦和正切,第二行包含第一行的三角函数的倒数:cosecant,secant和cotangent。
以下身份构成并且越来越荒谬。漫画反映了当我们更加强烈地使用这些身份时所产生的混乱,因为它们之间存在许多隐藏的依赖关系。您还可以通过各种三角公式检查它们的相关性。
第三和第四行是通过将三角函数视为变量而不是函数的乘积,然后使用上述身份来创建单词。例如sin = b /c – &gt; cin = b /s(这也可以是对C ++ cin的引用)。
倒数第二行在(tanθ)虏= b虏/a虏的单个字母上执行一些代数作为最后一行的设置。最后一行取公式距离= 1/2 a t“”来自物理学“并将其插入前一行的等式中,做一些代数用distance2替换t虏并将(na)虏扩展为nana到得到最终的等式,distance2banana = b鲁/胃虏。只有当三角运算符被视为变量乘积而不是运算符时,这才是有效的代数,但这是人们首次学习三角函数时遇到的常见误解。距离方程是一个恒定加速的物体在最初静止时在给定的时间长度t内移动的距离,最常用于找出物体在一定时间内从重力影响下落下的距离(或者如何多长时间才能达到给定的距离)。
如果您只是对六个标准三角函数进行代数操作,那么有一些公式会出错。
cas?= o /c似乎是从cos?= a /c得出的,但要从“cos”得到“cas”,必须除以“o”并乘以“a”。这将导致cas?= a虏/o c。
在身份认同中,其中一个“s”变成了“t”,然而这可能是通过“声音延伸”从“罪恶之二”的声音到达类似于“昆虫”这个词的声音。另一种可能的转换是如果你将“s”视为秒,那么“t”可以是时间,它与身份主题保持一致。
标题文字是字谜。由于乘法的可交换性(表明顺序不影响乘积),如果将这些等式视为如前所述的单个变量,则这些等式是等价的。添加了另一层荒谬,因为变量Theta被拼写出来并分成其字母,然后将其作为单个变量处理。 (这里所指的反正切是反正切,与切线函数的单边反转。你通常不会写,因为漫画中的theta指的是一个角度,而反正切的角度是一个角度,而不是它的论点;然而,在这里使用theta只是非常规的,不是禁止的。)反正切一般产生theta,它在theta上的意义很难被理解。兰德尔在这里通过诙谐的代数证明来阐明,采取第二次反正切的θ产生了神奇的效果。
从物理学(及其他)[编辑]
公式s = 1/2 a t gives给出了均匀加速物体随时间推移的距离。第二个公式属于天文学和开普勒第三定律,其中行星轨道周期的平方与其轨道的半长轴的立方成正比,意味着b3和t2的分数是常数(香蕉)。
但是使用角度θ作为论证导致理查德费曼,他做了许多着名的物理学讲座和他从1964年开始的关于太阳行星运动的遗失讲座,其中他只使用几何,基于轨道椭圆,一个圆圈和匹配的直角三角形来说明开普勒的这个定律。为了更深入地理解为什么它真的起作用,在“符号几何学杂志”上有一个很好的演示:费曼说:“ewton意味着开普勒,不需要微积分! (Brian Beckman,2006) – “/a>
漫画中代数错误的证明[编辑]
有些人试图争辩说,某些公式中的错误存在数学上的合理性,通过陈述(没有证明)你可以证明原始六个三角形身份的有效解决方案(其中字母被视为变量相乘)可以是操纵以表明解决方案必须具备
a = o和s = t。
这些证明不正确,可以通过反例轻松显示。如果您进行以下变量赋值,例如
o = s = 1/2并且设置c = e = 2而将其他变量设置为1(a = b = i = n = t =胃= 1)。此变量赋值将同时满足所有六个原始trig标识:
;
;
;
;
;
。
但是,在这个有效的任务中,我们有
以来
我们有。
这表明你无法进行有效的代数推导
要么
没有超出六个给定三角恒等式的额外假设。