Title Text:They’re robust against quantum attacks because it’s hard to make a quantum system that large
Origin:https://xkcd.com/2626/
https://www.explainxkcd.com/wiki/index.php/2626:_d65536
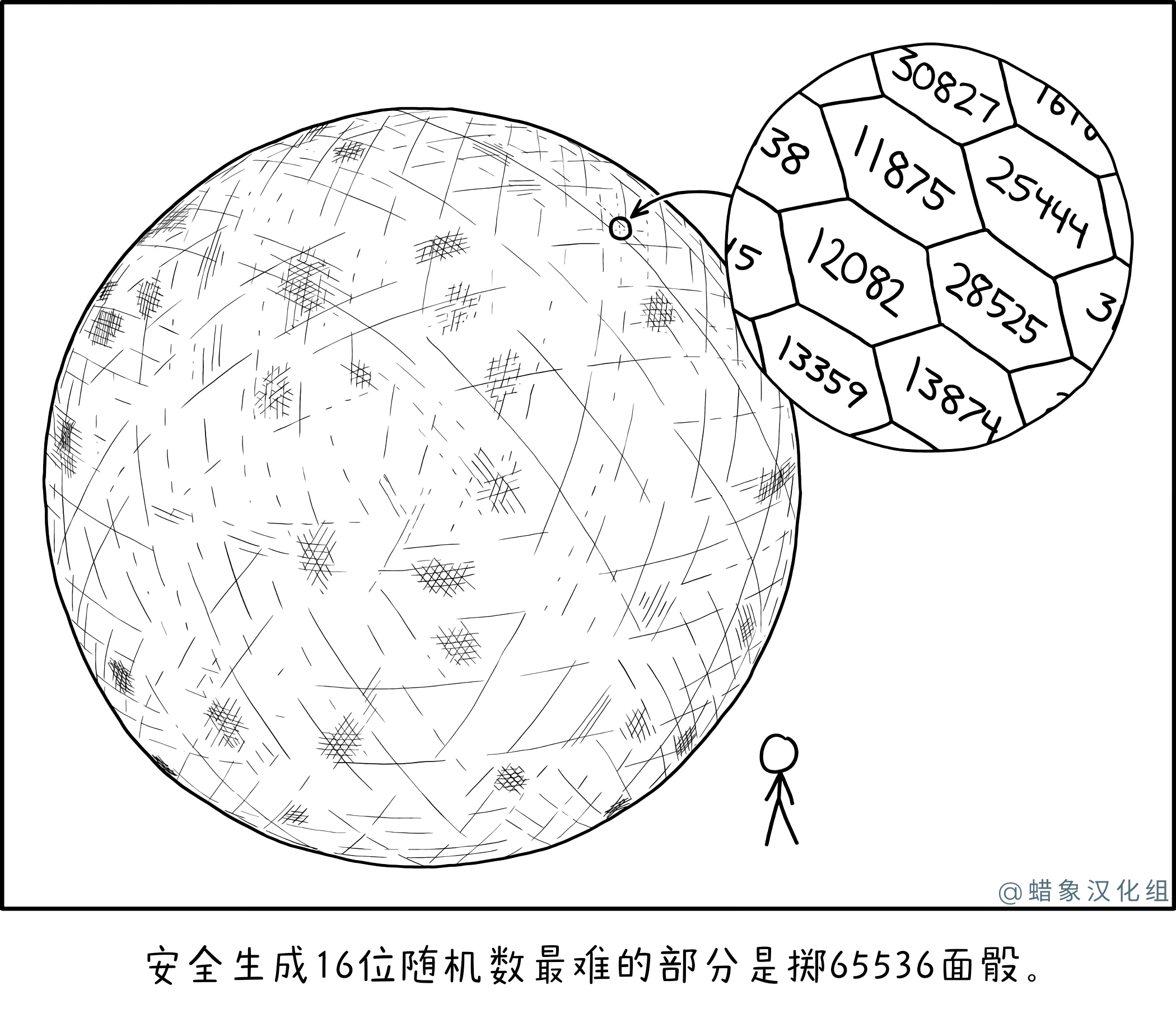
65536面骰
http://xkcd.in/comic?lg=cn&id=2626
在二进制计算中,16 位无符号数的范围从 0 到 65535,共有 65536 个唯一数,这个数字因此为软件工程师所熟知。以真正随机的方式生成大量数字是密码学中反复出现的问题,需要将私人消息发送给另一方。今天人们仍然使用 dierolls 来生成私人随机数。
在角色扮演游戏中(偶尔在其他桌面游戏中),经常使用多种形状的骰子来生成特定范围内的随机数。按照惯例,根据它们的面数将它们称为dn 。传统的六面骰子是 d6,许多流行的纸笔角色扮演游戏使用 d4 和 d20 之间的骰子。虽然桌面游戏中使用了较大的骰子(最常见的是 d100),但它们通常被分成多个较小的骰子。例如,一个 d100 通常是两个 d10 掷在一起,一个骰子提供第一个数字,另一个骰子提供第二个数字——可能组合的总数 (100) 是两个骰子面数的乘积 ( 10 * 10)。而“真正的” d100s和其他大数字骰子确实存在,大多数人认为它们是不切实际的:它们需要要么大得不切实际,要么具有非常小的面(导致数字的小字体),它们足够接近球体,这很难让他们进入一个稳定的休息位置,即使他们是静止的,用肉眼也很难确定哪张脸“在上面”。Zocchihedron (d100) 模具也难以确保无偏,因为几何形状需要不同的面,因此它可能落在每个面上的“停止因素”的不同混合。最大的无偏骰子是d120 (不包括双锥,理论上可以任意多面制作),因此Cueball很可能
在这里,Cueball 构建了一个 d65536 用于生成随机 16 位数字。它可能已经解决了用更少的骰子生成大量随机数的问题,但它把大量骰子的所有问题放大到了荒谬的极端。为了使面部可读,骰子巨大得离谱,使站在它旁边的人相形见绌。滚动这样一个模具不仅在物理上具有挑战性,而且如果结果是随机的,它还需要一个巨大的空间来滚动,并且这个空间需要有一个非常平坦和刚性的表面才能让模具来休息。即使这些问题得到了解决,仅仅站在有利位置看到骰子的顶部将是一个重大挑战,而确定哪个数字真正在顶部几乎是不可能的。如果真的想用骰子,简单地使用多个掷骰子会容易得多。例如,一个人可以掷 8 个 d4 骰子(或使用 16 次掷硬币),并将结果转换为二进制。这与单个掷骰具有相同的随机性[需要引用] ?,但可能需要更长的时间,所以人们购买 d16s 来简化它并加快它的速度。
与漫画中描绘的最接近的规则形状可能是戈德堡多面体。但是,不存在恰好有 65536 个六边形面的多面体。最接近的戈德堡多面体由 65520 个六边形和 12 个五边形混合而成,总共有 65532 个面。可以通过限制其可以着陆的侧面并将这些侧面设计为公平的来构建没有匹配规则形状的公平模具(例如,具有延伸其整个长度的矩形刻面的棱镜和圆形端部以确保它最终不平衡)。
标题文本提到了随着量子计算技术的发展,密码系统(尤其是 RSA 和其他基于因子分解的系统)如何容易受到量子攻击。标题文本本质上是对“大型”量子系统的想法的双关语。量子计算意义上的“大”大约是 64 个量子位,每个量子位最多是一个或两个原子。这仍然是微观的,永远不会像漫画所关注的巨型骰子那么大;但是对于观察良好的环境和没有足够熵的人类滚动(假设有人痴迷于某个数字将骰子放在柔软的东西上),传统计算机可以预测一些滚动。有关密码学的非数学路径, 另请参见538 。