Title Text:The combination croquet set/10-lane pool can also be used for some varieties of foosball and Skee-Ball.

Origin:https://xkcd.com/2625/

https://www.explainxkcd.com/wiki/index.php/2625:_Field_Topology

场地拓扑学

http://xkcd.in/comic?lg=cn&id=2625

场地拓扑学是数学中的一门学科，但在这部漫画中，兰德尔正在研究用于各种运动的运动场的拓扑结构。漫画描绘了这样一种情况，即多用途运动设施的普遍做法已由“拓扑部门”组织起来，并由所有正常运动场在拓扑上等效的运动项目共享。. 拓扑中的一个关键假设是您可以忽略相关对象的形状、大小和材料的特殊性。这形成了一个有趣的对比，因为“等效”的拓扑部门运动场实际上不太适合漫画中列出的活动，因为标准的定位、箍、网和杆的大小和形状以及场地本身的材料都不是相当于用于这些活动的真实运动场。

（不要与数学领域或菲尔兹奖混淆——尽管这个概念很可能是漫画中的一个双关语，因为数学（包括拓扑学）和大多数曾经能真正想象到的东西，大部分都是被执行的（“玩过” ) 在数学领域内。)

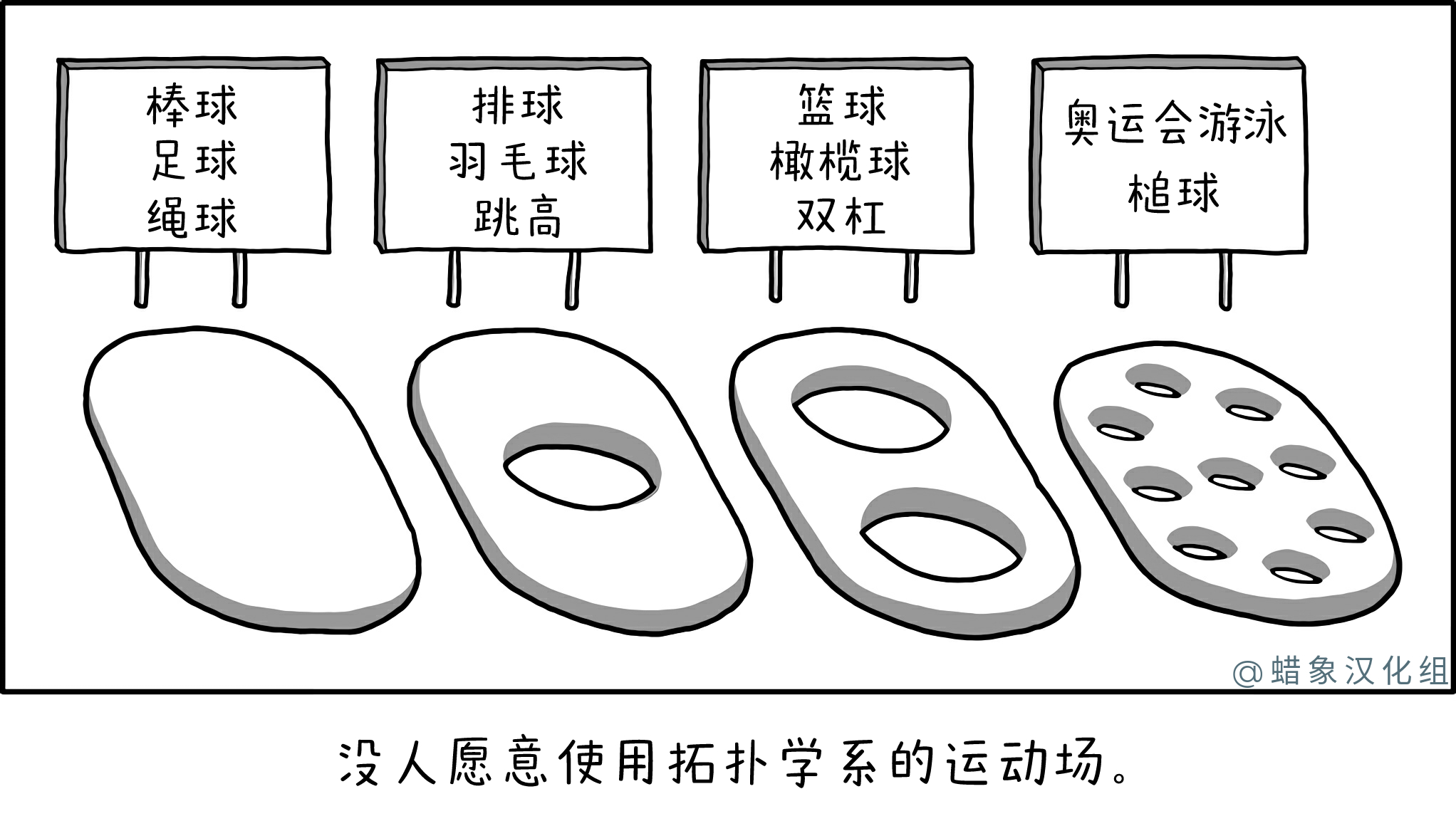
在拓扑学中，可以平滑地相互变形而无需添加或删除孔的形状被认为是等效的。拓扑洞是标称空间（或区域，或其他流形）的一个区域，受限于该拓扑的任何东西都不能通过该区域。环路是跨越拓扑（或通过它所描述的世界构成的可行电路）的允许区域的路径，最终到达它开始的地方。例如，当描述一个固体物体（如咖啡杯）占据的空间时，把手形成一个带孔的环。如果一个环不能被收紧（最终调整为采用更短的路径）到一个点，那么它必须围绕至少一个“拓扑洞”，并且你有单独的唯一路径（或点，即

在描述负空间时，例如拱门周围的空间，“洞”将是拱门本身的材料。这是因为围绕拱形材料任何部分的环形成的环只能缩短到有限的长度，而不是一个点；“洞”是迫使这些环存在的拱形障碍物。与地面相连的篮球架形成了一个类似的障碍物，其中有一个环穿过它，因此篮球架周围的空间包含一个等效的孔。在这部漫画中，拓扑部门根据比赛场地中此类障碍物的数量分析了进行各种运动的空间。然后，漫画中描绘的每个空间都标有在具有该数量洞的场地上进行的运动。

棒球、绳球和足球在三维空间中连续的场地上进行。这意味着可以穿过任何定义场的结构周围或上方的任何路径，而没有障碍物可以在它们周围的循环中穿过。足球场上的球门可能不会造成洞，因为球门柱和横梁通过网与球场相连；兰德尔显然认为这些形成了连续的表面，不允许循环通过它们。

排球和羽毛球是使用悬挂在杆子上的网进行的，跳高有一个让参赛者跳过的酒吧。由网或杆和支撑杆形成的结构可以被认为是一个穿过比赛场地的“洞”，因为在网/杆上方和下方形成一个环路的路径不能收缩到一个点，所以他们的比赛漫画中的田野都有一个“洞”。

一个篮球场有两个篮筐。双杠可以被认为是两个拱门。两者都有机会通过任何一个（或两个）结构，因此结构的材料在游戏“空间”的拓扑抽象中定义了一个洞。由于我们被告知这些运动场属于拓扑部门——并且不一定推广到所有运动场——我们可以假设他们的“足球”场要么用于橄榄球，要么用于使用 H 形立柱的美式足球。

一个奥林匹克规模的游泳池有 10 条泳道，因此有 9 条泳道分隔线固定在泳池的每端墙壁上，形成贯穿游乐区的拓扑洞。槌球中的每个箍类似地是一个穿过空间的洞。虽然大多数版本的槌球使用六个箍，但九个箍用于“后院槌球”，在美国和加拿大进行休闲演奏。拓扑部门忽略 了游泳池中的空间通常充满水的事实^{[需要引用] 。}

如标题文本中所述，最后一种配置也同胚于桌上足球桌（每根杆支撑桌子上方的玩家图形定义一个洞）或Skee-Ball 球道（更直接，因为它只是一个飞机上有几个可以扔球的洞）。这些“字段”实际上没有相同数量的孔，但显然被拓扑部门归为具有“许多”孔。

不幸的是，拓扑部门似乎没有跨栏事件的领域。