Title Text:You say this daily walk will reduce my risk of death from cardiovascular disease by 30%, but also increase my risk of death by bear attack by 300%? That’s a 280% increased! I’m not a sucker; I’m staying inside.

Origin:https://xkcd.com/2599/

https://www.explainxkcd.com/wiki/index.php/2599:_Spacecraft_Debris_Odds_Ratio

航空器碎片的比值比

http://xkcd.in/comic?lg=cn&id=2599

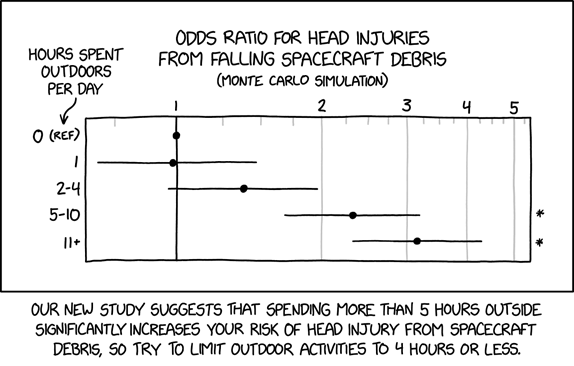
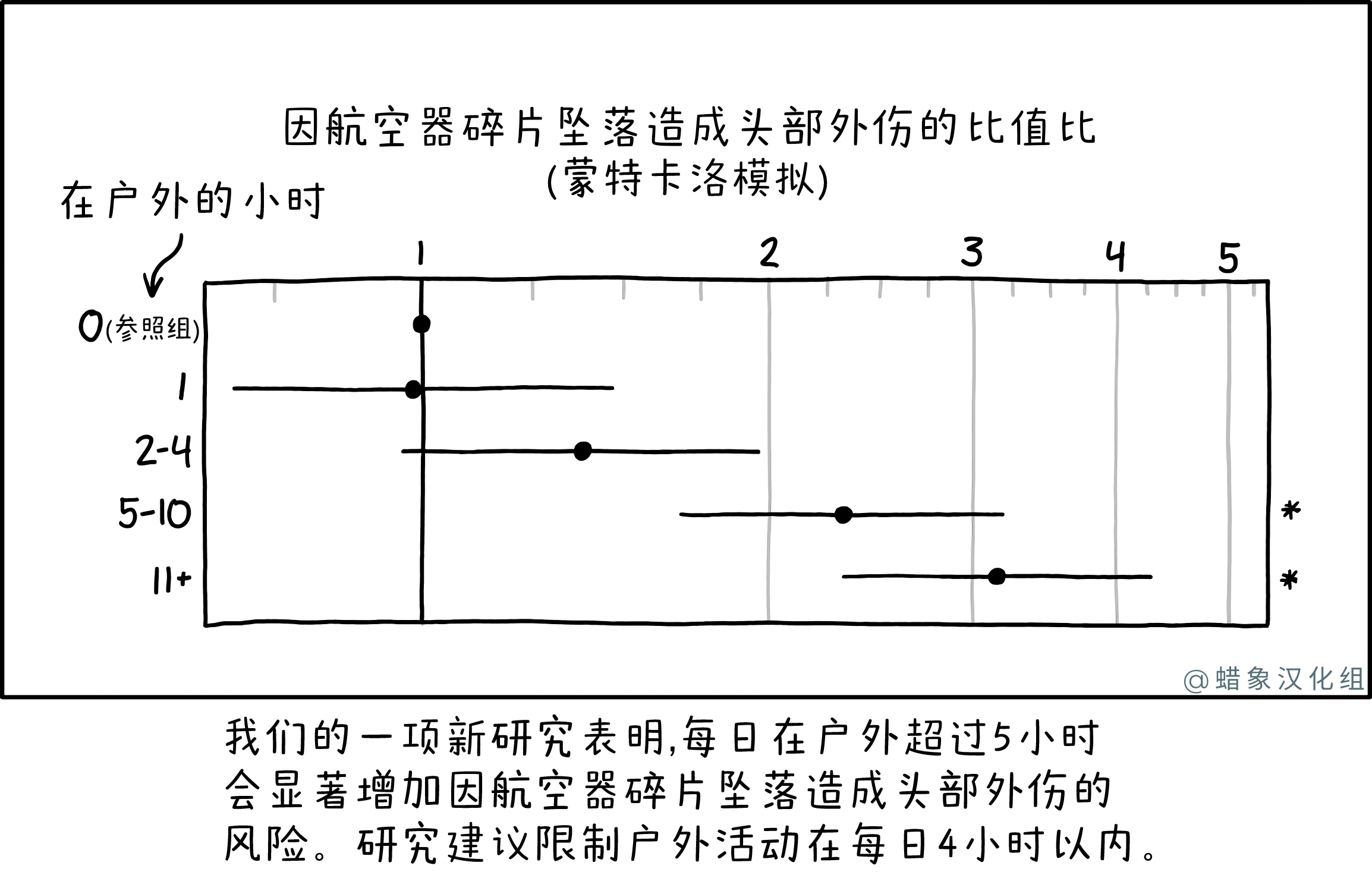
这部漫画是对统计数据的误解，与《 1252：风险增加》非常相似。它解释说，每天外出超过 5 小时会显着增加因航天器坠落而导致头部受伤的风险，并建议限制户外活动以避免这种风险。

然而，由于被坠落的航天器（任何部分）击中头部的几率一开始就很低，因此将其翻两番或更多仍然会导致可忽略不计的概率。时间大于 4 小时的水平误差条标有星号，表示它们与 0 小时的参考值有显着差异，因为实际上这些误差条不会与 0 小时参考值的垂直线重叠。

误差线是数据可变性的图形表示，并在图表上用于指示报告测量中的误差或不确定性。

按小时括号显示数据隐藏了每个括号内的数据分布。如果数据是按小时而不是按小时组呈现的，它们可能会显示不同的风险增加阈值或没有阈值（优势比可能是线性的）。

图表和误差线基于蒙特卡罗模拟，这是一种使用重复随机抽样来获得一系列结果发生可能性的计算算法；例如，参见这篇关于蒙特卡洛模拟的文章. 此外，这可能表明整个研究是通过蒙特卡洛模拟进行的，并且没有收集到真实数据，这增加了关于在户外花费更多时间可能导致航天器坠落导致头部受伤风险增加的说法的荒谬性。事实上，人类很少被航天器碎片击中，以至于模拟可能是研究风险的唯一方法。要获得重要的实验数据，需要一个荒谬的大样本量，在几十年内涉及数千万参与者。

对坠落航天器的具体提及可能是受到此漫画发布时间（2022 年 3 月）前后发生的事件的启发。大约在此消息发布前一个月，俄罗斯航天局负责人Roscosmos警告说，对俄罗斯的制裁（主要是针对2022 年俄罗斯入侵乌克兰的制裁）可能导致国际空间站坠毁。由于空间站的俄罗斯部分是提供推进力的部分（尽管它是为依赖其他部分产生的动力而建造的），所以这一点被认真对待，截至发布时，美国宇航局正试图提出万一情况恶化的替代稳定策略。最近也有报道在巴西发现的大约 600 公斤太空火箭碎片。

标题文本开了一个类似的玩笑。虽然外出时因熊袭击而死亡的机会增加大于因心血管疾病而死亡的机会减少，但通过外出锻炼，以这种方式将它们结合起来是不正确的，因为心血管疾病的死亡率要高得多。开始死亡的机会，将其减少 30% 对整体预期寿命的影响比将因熊袭击而导致的非常小的死亡机会增加四倍要显着得多。至少对于我们大多数不住在野熊自然栖息地或附近的人来说。

标题文本的“280% 增加”也是一个错误，尽管可能不是因为起初显而易见的原因（例如，正确的计算不是“300% – 30% = 270%”）。“增加 300%”意味着将概率乘以 (1 + 3.0) = 4.0，而“减少 30%”意味着乘以 (1 – 0.3) = 0.7。结合这些意味着将两者相乘，总变化为 4.0 × 0.7 = 2.8，即 280%。但是，此结果意味着风险已增加到其旧值的280%，而不是280%。无论如何，像这样简单地将两种截然不同的风险结合起来仍然是无效的。

赔率和赔率[编辑]

事件的几率是它发生的概率除以它不发生的概率。人们经常将赔率表示为比率（例如，在 6 面骰子上掷出 6 的赔率可能表示为 0.16777… : 0.83333…，或等效为 1:5），但重要的是要注意这样的比率不是优势比（将其称为“概率比”是合适的，但这个术语不是标准的）。

优势比是事件 O 发生的几率，假设其他一些事件 E 已经发生，除以 O 的几率（假设 E 没有发生）。O 有时被称为“结果”，E 有时被称为“暴露”，因为人们经常有兴趣比较诸如在您吸烟 (E) 的情况下患肺癌的几率 (O) 与患肺癌的几率之类的事情假设你不吸烟，作为衡量暴露于 E 对结果 O 的影响程度的一种方式。在漫画的情况下，结果变量 O 是因坠落的航天器碎片而头部受伤的事件，并且暴露变量 E 是每天在户外花费 H 小时的事件，对于 H 的各种值。漫画似乎是说，对于 H 的每个值，E 有两个选项：

所以对于 H 的小值（例如每天 1 小时），漫画是说被航天器碎片击中的事件或多或少独立于每天在外面花费 H 小时的事件，也就是说，几率无论您在每天花 H 小时在户外还是从不外出之间做出选择，被击中的风险或多或少都是一样的。因此 1 小时柱上的点接近 1，因为这两个几率或多或少相等（点似乎代表优势比的平均估计值）。

请注意，在计算这部漫画的赔率比时，分母中的赔率总是相同的，因为它们是在你从不出门的情况下被击中的几率，这不取决于 H。所以当漫画说H={11+ hours per day} 的几率高于 3，这实际上是说当你在户外度过这么多时间时被击中的几率是你在 1 小时内被击中几率的 3 倍多一点每天在外面。

假设被击中的概率是：当你每天在户外待 1 小时时为 P，当你每天在户外待 11 小时以上时为 Q。这两种曝光下被击中的几率分别是P/(1-P)和Q/(1-Q)，而且因为几率比的分母相等，所以漫画说Q/(1-Q)=kP /(1-P)，其中 k 略大于 3。如果我们重新排列它以获得 Q 的表达式，我们得到：

      Q/(1-Q) = kP/(1-P)
<=> Q(1-P) = kP(1-Q)
<=> Q-QP = kP-kPQ
<=> Q+kPQ-QP = kP
<=> Q(1+kP-P) = kP
<=> Q = kP/(1+kP-P)
<=> Q = P/(P+(1-P)/k) {将分子和分母除以 k}

由于 P 小到可以忽略不计，所以 1-P 非常接近 1，而 P+(1-P)/k 非常接近 1/k。因此，Q 非常接近 kP（即 P 的 3 倍多一点），这意味着当您每天在户外度过 11 小时以上时，被击中的概率仍然可以忽略不计。因此，漫画中关于我们根据估计的优势比在户外呆 4 小时或更短时间的建议是非常错误的。