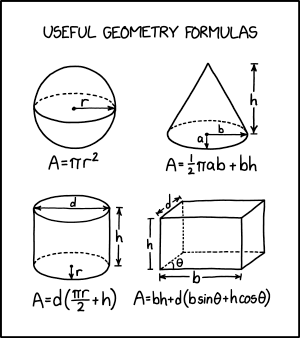
Title Text:Geometry textbooks always try to trick you by adding decorative stripes and dotted lines.
Origin:https://xkcd.com/2509/
https://www.explainxkcd.com/wiki/index.php/2509:_Useful_Geometry_Formulas
几条有用的几何公式
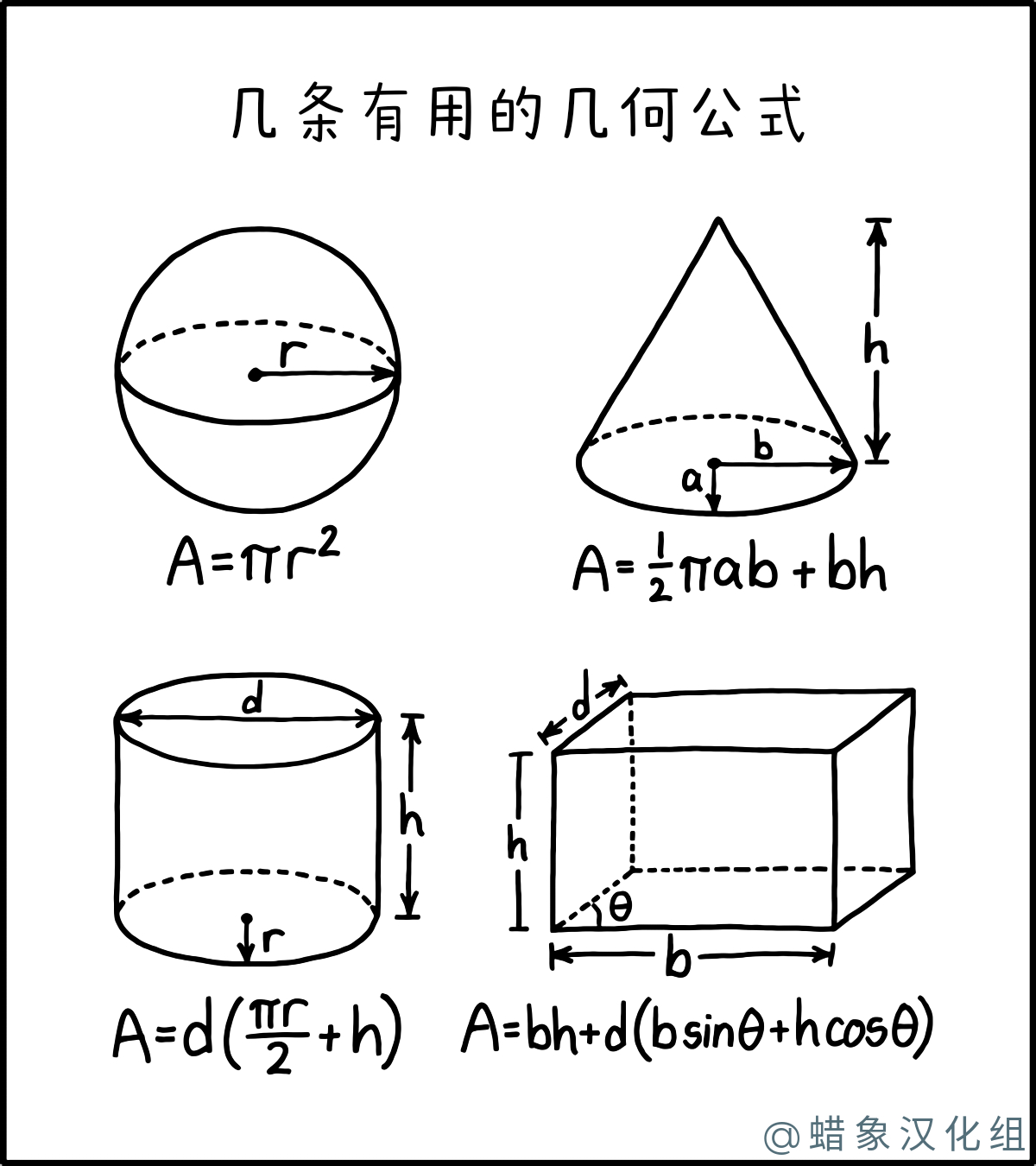
注释: 图上的公式作为平面图形的面积计算都是正确的,但是加上装饰条纹和虚线后,很容易看成立体图形的表面积计算。
http://xkcd.in/comic?lg=cn&id=2509
这部漫画展示了四个二维几何图形的面积公式,每个图形都有额外的虚线和/或实线,使它们看起来像 3 维物体的插图。第一个是圆的面积的简单方程,第二个是底为半椭圆的三角形的面积方程,第三个是底为椭圆的矩形的面积方程,第四个是由两个相对的直角和连接它们边的两条平行对角线组成的六边形面积方程。在每种情况下,只计算每个形状的轮廓形成的面积。
类似的插图常见于几何教科书中,用于在二维页面上描绘三维图形。它们通常使用斜线表示向远处后退的边缘,并使用虚线表示被实体的较近部分遮挡的边缘。开玩笑的是,这里给出的公式是针对每个二维形状在其外部实线内的面积,而不是针对图示 3D 对象的表面积或体积(如几何教科书中所示)。标题文本继续这个笑话,声称虚线只是装饰性的。
插图描绘了以下平面或立体图,具体取决于解释。
- 左上角 – 带有内切椭圆或球体的圆
此图通常用于描绘 3D 球体,椭圆表示通过中心的“水平”或轴向横截面;椭圆的实心下半部分代表该横截面圆周的“前部”,而虚线上半部分代表同一截面的“后部”,如果这是实心形状,则该部分会被遮挡。
圆的半径,从中心到它与椭圆相交的右边缘,标记为“r”。在球体的教科书图中,半径可以用从中心到椭圆上不同点的对角线来标记,这意味着该横截面上的所有点,实际上是整个球面上的所有点都在中心半径相同。但是,页面上的这条线会比实际半径短,因此对于 2D 外部形状的面积公式毫无用处。
页面上二维形状的面积就是圆的面积,即 A = πr 2。这是图下方的标题。
巧合的是,3D 球体的水平横截面面积(如椭圆所示)也是 πr 2,熟悉此类图表的读者最初可能会认为这就是其含义。然而,这并不扩展到其他数字。
该图通常描绘的 3D 球体的体积为4 / 3 πr 3,表面积为 4πr 2。
- 右上角 – 带有对称对角线的椭圆或圆锥
此图常用于描绘 3D 直角圆锥,椭圆的下半部分代表底面的“前缘”,上半部分代表被遮挡的“后缘”。然而,这样的图纸通常不会同时使用“a”和“b”来描述圆锥底的半径,由于缩短,圆锥被绘制为椭圆。或者,该图可以描绘一个正椭圆锥。
Randall 将页面上 2D 形状的面积近似为由椭圆的长轴和两条线形成的三角形的面积与椭圆面积的一半 ( π / 2 ab) 之和,因为大多数椭圆的上半部分与三角形重叠。这个面积的方程是 A = 1/2 πab + bh。这是图下方的标题。
圆锥图片的实际面积不是 Randall 的近似值,因为边在椭圆上的点处连接,在这些点上它们可以展开最宽并与椭圆形成切线,而这些点比定义长轴的点稍高. 这在 h 仅比 a 大一点的情况下最为明显。面积可以计算为正好 A = b (a arccos(-a/h)) + √(h 2 -a 2 ))。
该图通常描绘的 3D 直角圆锥体的体积为 πr 2 h/3,其中 r=a=b。“下”表面的面积为πr 2,而上圆锥面的表面积为πr√(h 2 + r 2 )。这些面积都与漫画中的标题不相符,总表面积(这两者的总和)也不符合。
如果我们不假设 a = b,这张图也可以描绘一个正椭圆锥。椭圆锥的体积为π / 3 abh。下表面的面积为 πab,弯曲的上表面的面积为
2a√(b 2 + h 2 ) 0 ∫ 1 √( a²h²(t²-1) – b²(a²+h²t²) / a²(t²) -1)(b²+h²) ) dt。
- 左下 – 垂直连接的两个椭圆,或圆柱体
此插图通常用于描绘 3D 圆柱体或直角圆柱体。在这种情况下,上椭圆表示顶部圆形表面的“可见”部分,由于透视缩短,其“深度”小于其“宽度”,下椭圆的下部表示圆形表面的“前”边缘。下表面;下椭圆的虚线一半代表下表面被遮挡的“后”边缘。
更令人困惑的是,上椭圆的长轴标记为“d”,通常表示圆形表面的直径,而下椭圆的长轴标记为“r”,同样表示半径,即使绘制的椭圆既没有直径也没有半径。表示高度的“h”也用于矩形和实体对象。虽然在这种情况下 ‘d’ 是 2D 形状的面积计算所必需的,但在教科书中只能标记 ‘r’ 并且箭头可以在对角线上偏移而不是与任何图形轴对齐,以暗示其适用于半径的任何角度。
二维形状的非重叠部分由两个椭圆的长轴和垂直线形成的矩形,加上顶部椭圆的一半和底部椭圆的一半组成。矩形的面积为dh,长半轴为d/2,短半轴为r的椭圆的面积为πrd/2。总面积为 A = d(πr/2 + h),如图下方的标题所示。
3D 直角圆柱体(圆柱体)的体积为 πr 2 h,表面积为 2πr 2 + πdh,或 2πr(r + h),因为在这种情况下 d = 2r。每个平面的面积为 πr 2。如果我们不假设 d = 2r,那么右椭圆圆柱的侧表面积为 4h 0 ∫ 1 √( 1 – t²(1-4r²/d²) / 1 – t² ) dt。体积为π / 2 rdh。
- 右下角 – 平行六边形或棱镜
此插图通常用于描绘直角棱镜,其中“b”表示“宽度”,“d”表示“深度”,“h”表示“高度”。然而,标记的角度 θ 是 2D 形状的面积计算所必需的,通常不会用于直角棱镜的图中,因为所有角度都被假定为直角。假设“底”平行四边形与“正面”垂直,并且唯一的非直角是 θ,可以通过此图准确描述菱形棱柱。在那种情况下,’d’ 将不能准确地描述固体的深度,它实际上是 d sin θ。
2D 形状的区域由左下方的矩形、上方的平行四边形和右侧的平行四边形组成。表示棱镜正面的矩形面积为 bh。上平行四边形的面积是db sin θ。右平行四边形的面积是 dh cos θ。该区域的方程为 A = bh + d(b sinθ + h cosθ),如下图所示。
棱镜的表面积为 2bh + 2db sin θ + 2dh。体积是 bdh sin θ。假设是 3D 形状,θ 可以通过投影人为改变;可以假设 θ 为 90 度,sin θ 为 1(因此可以从公式中删除),但由于 θ 被标记,因此这种假设可能无效。
在计算机生成 3D 图形的发展历史中,计算体积投影所占据的表观视觉区域可能在类遮挡优化中很有用,其中每个绘制的像素可能会通过许多片段着色器。