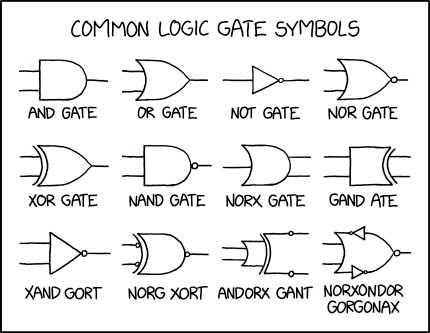
Title Text:In C, the multiocular O represents the bitwise norxondor gorgonax.
Origin:https://xkcd.com/2497/
https://www.explainxkcd.com/wiki/index.php/2497:_Logic_Gates
逻辑门
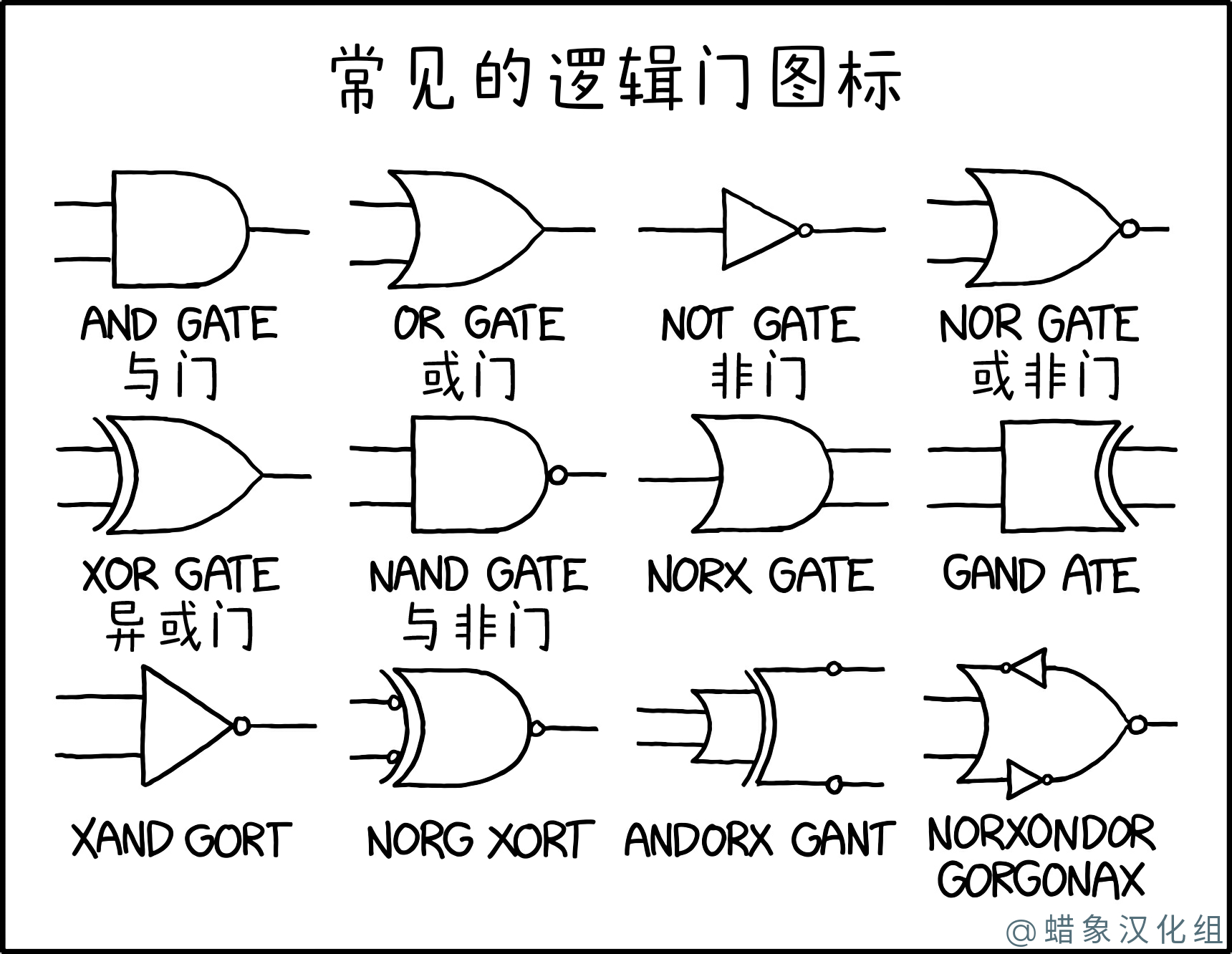
脚注:
多眼O:ꙮ是西里尔字母О о的其中一种变形。古文字学家叶菲姆·卡尔斯基在1429年刻的一部诗篇的副本中最早找到并记录下这个字母,现在则能于谢尔盖圣三一修道院见到这份手稿。
http://xkcd.in/comic?lg=cn&id=2497
漫画列出了逻辑门。前六个是真实的,但后六个是虚构的,并且变得越来越荒谬。这最后六个的名称由与前六个相同的字母和音节组成,以便一目了然以符合它们的命名约定。
一些看似不可能的门部分组合方式可以在读者的脑海中引发关于量子计算如何涉及同时处理多种可能性的想法,或者机器学习如何涉及从输出到输入反向求解系统。这些名字越来越深刻地呼唤着一些神话般的灾难。
| 姓名 | 解释 |
|---|---|
| 与门 | 当且仅当两个输入都为真时,与门才会输出真。(输入 1和2 必须为真。)按照惯例,它是一个具有扁平输入端通向半圆形输出端的符号。 |
| 或门 | 如果一个或另一个或两个输入为真,则或门输出真。(输入 1或2 可能为真。)按照惯例,它是一个具有凹入输入边缘的符号,它通向类似于哥特式尖拱的输出端,转向向前。 |
| 非门 | 当且仅当输入为假时,非门输出真。(唯一的输入不能是真的。)隔离非门的惯例是一个三角形(让人联想到二极管或运算放大器比较器),它明显指向逻辑通道的方向,并带有一个圆圈。 |
| 或非门 | 当且仅当两个输入都为假时,或非门输出真。(均未1也不2必须是真实的;交替解释为它必须ñ OT是真实的,是1或2为真)。该符号是其尖端带有非圆的 OR 形状。 |
| 异或门 | XOR(“异或”的缩写)门在一个或另一个输入为真时输出真,但不是两个输入都为真。(相互ê X cusively,无论是1或2必须是真实的。)这个符号是标准的 OR 符号,但有一条凹线与通常的略有不同,以连接到输入线以区分其更具辨别力的行为。 |
| 与非门 | 如果输入中的一个或另一个或两个输入为假,则与非(“非与”的缩写)门输出真。(它必须Ñ OT是真实的,同时为1和2都为真。)符号是与门,其尖端带有非圆。 |
| NORX门 | 甲单个馈线引线成标准OR式输入端,而两行被视为从一个AND式输出前的情况。如果门仅遵循 AND 逻辑,并且输入在内部没有为此目的重复,那么结果将始终为假。
如果门使用 OR 逻辑和/或输入在内部用于两个传统要求的输入,则输出将完全是原始输入的状态。 两个输出似乎是重复的(与 Out 和 Not Out 配对不同),因此整体效果可能是充当无干扰的“分离器”门。 或者,如果单个输入携带两个信号的叠加(请参阅下面的 NORG XORT),那么这可能会被拆分为两个输入,在内部进行处理(可选地在分离的输入上进行 AND 和 OR 结果的新叠加)并传播继续进入两个不同的、故意解开的(但可能仍然是每个叠加的)输出,以进行进一步的量子处理。 (图中没有 NOT 类型或 XOR 类型的元素,但值得注意的是它是“XNOR Gate”的部分重新排列的字谜。) |
| 甘德吃了 | 两个输入馈入 AND 型接收端。假定的输出端具有镜像 XOR 输入设计,带有两个向前的连接。假设它仍然接受来自左侧的输入并产生右侧的输出,则该门最初可能充当内向对的与门,但随后(随机?)生成输出信号,作为 XOR 的输入,产生相同的输出。即,如果两个输入都为真,则两个输出配对为一个为真,一个为假(以任一顺序);对于任何其他输入,两个输出都处于相同且相同(未指定)的逻辑状态。
(这个名字是“AND Gate”的一个词,但可能没有其他意义。) |
| XAND 戈特 | 两个输入非常规地输入到传统单输出的完美标准非符号中。单个 NOT 如何处理两个输入并合并它们并不明显。现有的两输入门已经满足了所有明显的功能。也许它在逻辑上与 NOR 门相同,但绘制和命名以表达其性质为“非 A 和非 B”,而不是不太直观的等价物“非(A 或 B)”。
或者这可能是为了创建(然后反转)两个奇异输入馈送的组合量子叠加,因此充当一种信号多路复用器。 (这个名字似乎只是与功能的绘制元素相关的门名称无关紧要。“Xand”是“亚历山大”这个名字的一种常见形式,有时因其引人注目的“X”而被用于奇幻小说中的主要人物,而“Gort”是在电影《地球停转之日》的各种版本中出现的一个特别强大的外星机器人的名字。然而,这些事实都可能没有真正的相关性。) |
| NORG Xort | 初始输入端类似于 XOR 门,但具有“否定”节点,非常规地位于输入向内引导的位置。输出端具有NAND外观。与处理直接输入的方式相比,XOR 门最终不应对预先否定的两个输入做出任何不同的反应,但 NANDness 的承诺可能不会使事情变得如此简单,而不会偏离量子逻辑的可能性(如上面建议),其中可能“仅仅”理解起来非常复杂。
(给出的名称引用了 NOR 和 XOR,但可能完全脱离了对其逻辑含义的任何逻辑解释。) |
| 安多克斯甘特 | 两个输入似乎馈入 OR 接收端,但这会转变为馈线进入后续 XOR 接收器,后者又转变(没有输出上限)到两个输出轨道,每个轨道都有一个“孤立的”NOT-节点在他们身上。一般来说,它可以被解释为一个或门,其内部结果被发送到一个输出轨道,而相反的结果被输出到另一个轨道,然后两者都被反转。或者,在这种情况下,量子(重新)叠加和分离可能再次以难以缩小的方式起作用。
(名义上的标题进一步缺乏明显的逻辑,从 XOR 和 AND 的可能重新排列开始,然后是插入 N 的部分 GATE。“Gant”可能是对特定运动服装制造商/零售商的引用。有,当然,还有甘特图。) |
| NORXONDOR 戈尔戈纳克斯 | 两个输入通向一个类似 (N)OR 的入口,在恢复作为 NOR 门输出端的绘制目的之前,其连续侧重新用作连接器,引导通过一对完全反平行的非门。如果要认真对待它们,那么特殊放置的 NOT 可能充当某种双向信号滤波器/整流器的指示。
(然而,门的名称是一个奇怪的构造,甚至可能与幻想/神话参考相呼应,例如刚铎和戈尔工。) |
现实生活中唯一被省略的逻辑门是 XNOR 门(“eXclusive Not OR”的缩写;它比较输入,当且仅当它们相等时,才输出真)。请注意,如果“NORG XORT”门被倾斜以匹配其独特的 XOR 样式的尾部,那么它在逻辑上将与它等效,因为它将是一个在两个输入上都带有 NOT 的 XNOR 门,这种修改对逻辑,因为它只是切换它需要的排他性的情况,而不关心它可能响应哪个版本的相同输入。
输入上的 double-NOT 将再次产生相同的输出(…如果输入不正确)。两个预应用到 (N)AND 或 (N)OR 的 NOT 将产生与 (N)OR 或 (N)AND 的(进一步)NOTted 版本相同的输出,相反(…如果不是-1并且 不是-2 那么这也意味着既不是 1也不是2)。通常这会在必要时显示为导入输入上的完整非门,但是(参见下面的 Transcript 和上面的 NORG XORT 描述)快捷元素偶尔会用于进一步的混合’n’匹配符号系统(与以“可理解”但绝对非标准的方式将连接线重新解释为部分形状边缘,反之亦然。
随着连接器和形状边缘线的故意混淆,在几种情况下也使用方向性,输入“端”可能也在(隐含的)输出端和反向子符号暗示具有子结构反馈的复合门,或者可能双向逻辑路径上的二极管整流。
很像2360: Common Star Types,随着列表的进展,这些名字开始听起来更像神话中的生物,最后是“Norxondor gorgonax”。与符号系统一样,名称似乎是标准名称的无意义重组(在某些情况下,可能是主题外的灵感)但通常与符号(误)使用不匹配,例如名称中的 X 不是暗示/被 XOR 的独特绘制特征暗示。
在标题文本Randall声称,在编程语言 C 中,多目 O (ꙮ) 字符,西里尔字母 O 的异国字形变体,用于表示最后一个运算符 Norxondor gorgonax 的按位版本(大概 ꙮꙮ 表示非-按位版本),适合作为多眼 O在一些宗教文献中用于指代“多眼六翼天使”(天使)。蛇发女妖(米色或其他颜色)的头上覆盖着蛇而不是头发,因此拥有多只眼睛,最著名的是美杜莎(在1608年描绘:气垫板)。ꙮ 角色抽象地激发了像克苏鲁神话中的那些伟大的超凡脱俗恶魔的想法。
C 是一种低级编程语言,因此它有许多与逻辑(即按位)操作相对应的操作。这些与以非按位方式工作的操作形成对比。例如,“&&”是将操作数作为一个整体的非按位“AND”运算符,而“&”是按位“AND”,它在吐出新的单个组合之前独立地组合其两个输入的相应位输出位代表的值。在非按位运算中,0 始终表示“FALSE”,而任何非零值都表示输入为“TRUE”,1 用于表示输出为 TRUE。因此,“14 && 3”给出结果 1:TRUE AND TRUE -> TRUE。在按位运算中,使用相同的值,
1110 = 14 & 0011 = 3 0010 = 2