Title Text:It’s not my fault I haven’t had a chance to measure the curvature of this particular universe.

Origin:https://xkcd.com/2205/

https://www.explainxkcd.com/wiki/index.php/2205:_Types_of_Approximation

没有机会测量这个特定宇宙的曲率又不是我的错。

http://xkcd.in/comic?lg=cn&id=2205

在物理学和工程学中，解决问题通常需要近似值，因为宇宙的物理特性可能难以建模。例如，在物理入门课程中，理论是在无摩擦的环境中介绍的。计算或近似中所需的精度级别取决于上下文。

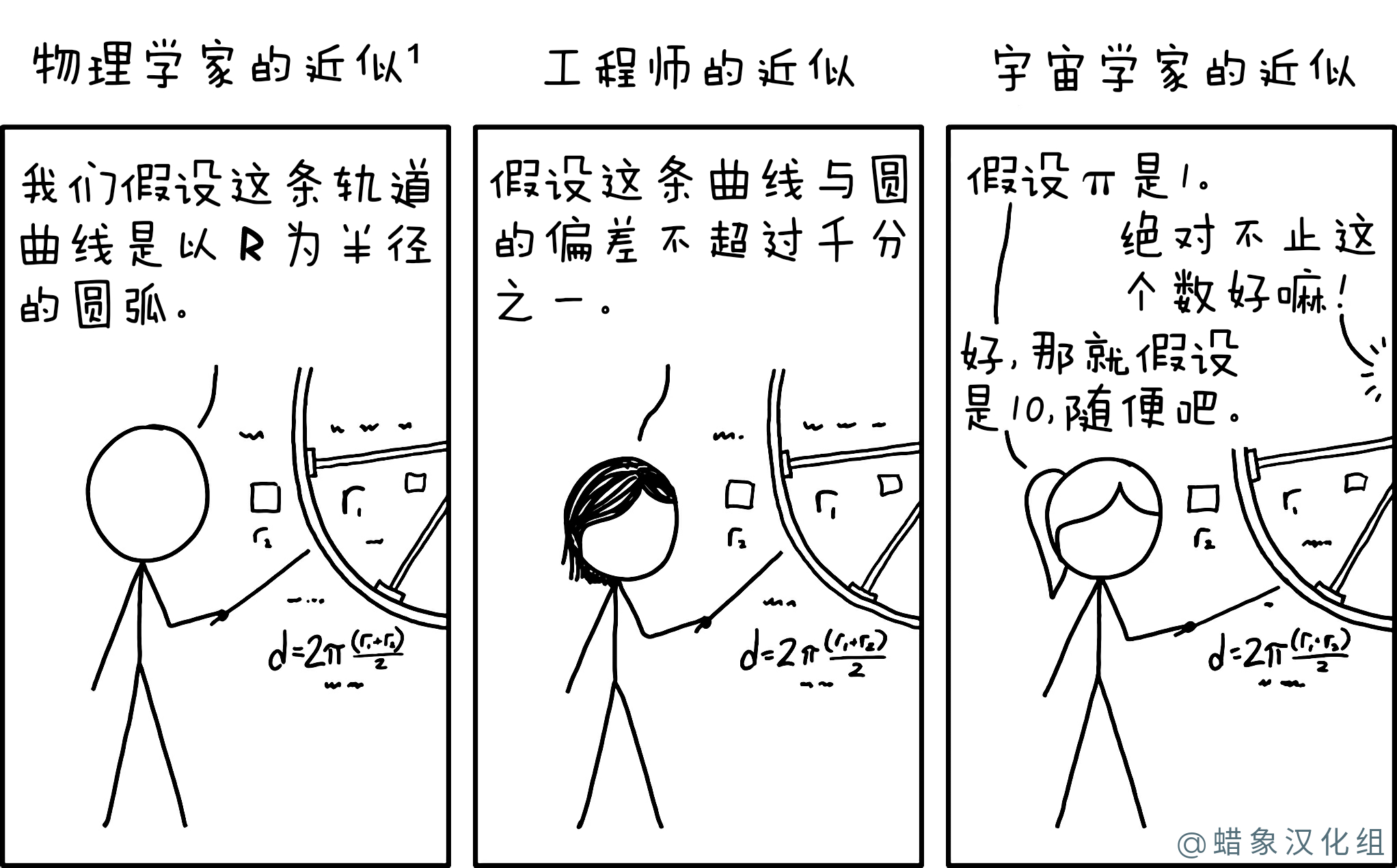
在漫画中，物理学家Cueball通常处理可以使用相对简单的数学运算的理论构造，并提出了一个问题，假设特定曲线是半径为R的（完全）圆弧。工程师必须处理与真实形状不同的真实事物。尺寸可能具有一定的公差。工程师Megan还假定曲线类似于圆，偏差因子为1/1000或更小。

当宇宙学家马尾辫使用的pi（π）精确度远不如1 时，就产生了笑话。

马尾辫提出用10代替1来暗示费米近似，如“ 画地球”中所示。数字以10为底的对数刻度舍入到最接近的数量级（1、10、100等）。在这个规模，“半途而废” 1到10之间是√ 10 ≈3.16。因此，将约0.316和3.16之间的数字四舍五入为1.，将3.16和31.6之间的数字四舍五入为10，依此类推。Pi是一个无理数，可以近似为3.14，因此它非常接近3.16截止点。最接近pi的数量级是10 ⁰或1。但是使用这种形式的估计，对pi而言，将pi近似为1还是其他合理的Fermi近似值10 ¹或10 并不重要。

Pi定义为圆的周长除以其直径的比率。此数字以3.14159开头，是不合理的值，该值是平面几何图形中此比率的值。但是在弯曲的空间中，该比率可能会有所不同。标题文字利用了这样一个事实，即几乎每个数字都可以是该比率，具体取决于圆所处的空间的曲率。宇宙学家不知道“这个特定宇宙”的曲率（一种有趣的陈述宇宙的方式宇宙学家居住的地方，它不是很平坦），因此pi并不是圆的周长与直径之比的最佳值。

这部漫画是对宇宙学趋向于在其工作中使用更粗略的近似的模仿，这会使工程​​师，其他物理学家，数学家等感到恐惧。总的来说，宇宙学家处理的距离，时间跨度，质量等如此之大，由于估算误差如此之大，以至于在其他地方都是荒谬的近似仍会在宇宙学中产生有用的答案。当处理宇宙学中的大量数字时，较小的乘法因子（例如3）消失为舍入误差：10 ¹⁰⁰和10 ^100.497之间可能没有有用的区别，即使这些数字相差非常接近pi的一个因子也是如此。该错误将极大地困扰大多数物理学家和工程师。

pi近似为1时，也可能是指天文学家改变测量单位以使宇宙的重要常数（例如光速或引力常数）等于1的习惯，这极大地简化了公式而不会影响数学。但是，数字pi是无量纲的比率，它不依赖于度量单位。