Title Text:…an effect size of 1.68 (95% CI: 1.56 (95% CI: 1.52 (95% CI: 1.504 (95% CI: 1.494 (95% CI: 1.488 (95% CI: 1.485 (95% CI: 1.482 (95% CI: 1.481 (95% CI: 1.4799 (95% CI: 1.4791 (95% CI: 1.4784…<
Origin:https://xkcd.com/2110/
https://www.explainxkcd.com/wiki/index.php/2110:_Error_Bars
誤差線
此解释可能不完整或不正确:由INFINITE系列错误栏创建。读者显然根据他们的统计专业知识开发了三种不同的观点。视图应单独列出(请参阅注释)。请勿过早删除此标记。如果您可以解决此问题,请编辑该页面!谢谢。
在统计图表和图表中,通常包括显示实际值与所示值的可能变化的误差条(或显示的值的可能误差)。由于在任何给定的测量中始终存在不确定性,因此误差条有助于观察者评估所显示数据的准确程度,或者如果真实值在可能的误差范围内而不是所示的确切值的影响。有计算误差线的统计方法(它们可以显示标准偏差,标准误差或置信区间),但有多种计算方法的事实 – 加上对统计方法的一般不熟悉 – 意味着人们常常误解或误解了他们。
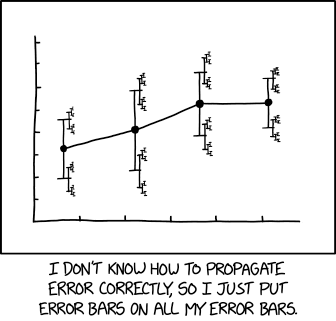
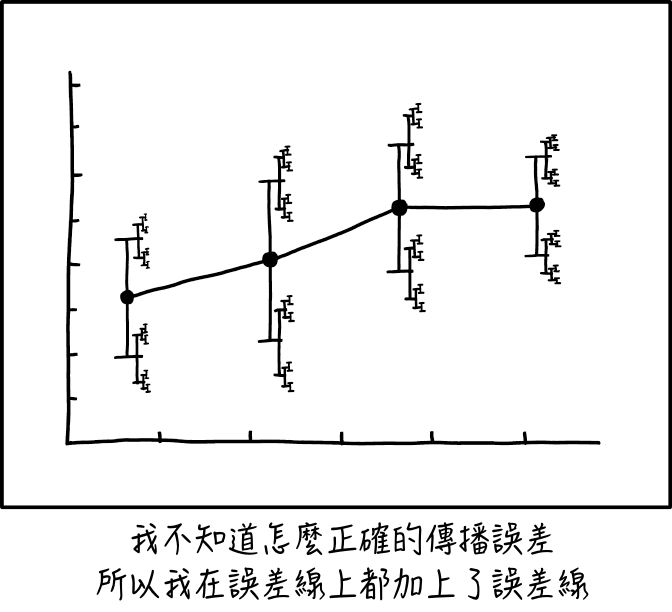
由于图表可能是经过数学处理的数据,因此还必须对数据处理来自记录过程的已知误差,以确定最终结果中可能出现的错误。数据的不同变换导致错误的不同变换,并且所使用的变换的正确性有时可能取决于源数据的分布的细微差别。不知道如何正确地传播他的错误,Randall反而将错误条放在他的错误栏的末尾,以反映错误已与其他错误相结合的事实,或错误条也有不确定性的事实或错误本身。但是,由于他的第二个误差条计算也是可疑的,他在它们上面放了第三组误差条。这无限重复,创造了一个类似于康托尔集的分形。
在标题文本中,他指出效果大小为1.68并且跟随它的95%置信区间(可能值的范围具有包含真值的95%估计概率),这通常由类似的东西表示“1.68(95%CI 1.56 – 1.80)。”由于他表示那些界限是不确定的,他从“1.68(95%CI 1.56”开始,然后将95%CI置于该区间的下限,“95%CI 1.52”,然后是下限值,“95%CI 1.504”,依此类推。在使用省略号之前,他深入11层。
通常,没有足够的数据来计算误差线上的误差线。被测量的数据具有分布,例如,一个人可能会对1,1,1,1,1,1.4,1,1,0.5,1和1的某些东西进行十次测量,这表明它可能接近1,因此可能存在一系列值是。但是,诸如平均值和标准偏差之类的属性本身不具有范围。如果一个人不确定是否已正确计算出这些数据,那么就没有足够的数据以任何有意义的方式计算一个人自己的技能不确定性;可以在错误条上声明错误条,如本示例所示,但这些只是猜测,没有统计上有用的支持。