Title Text:Protip: Any two-axis graph can be re-labeled ‘coordinates of the ants crawling across my screen as a function of time’.<

Origin:https://xkcd.com/1230/

https://www.explainxkcd.com/wiki/index.php/1230:_Polar/Cartesian

https://app-xkcd-cn.appspot.com/

这部漫画讲述了阅读极坐标图和更常见的笛卡尔坐标图之间的区别。

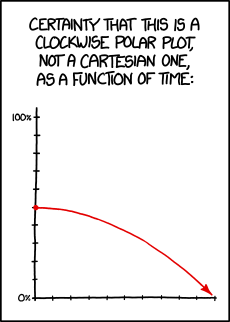
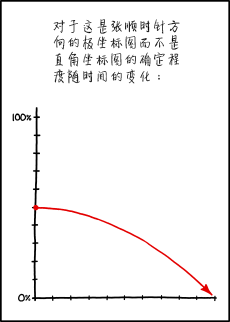
该图表旨在显示观众心中的确定性，它是一个顺时针极坐标图，作为时间的函数。

如果被视为笛卡尔图，则y（垂直）轴表示“确定性”，而x（水平）轴表示“时间”。图上的每个点由两个坐标表示，即x值和y值。随着时间的推移，我们向右移动，看到50％的初始确定性逐渐降低到零。也就是说，经过一段时间后，我们确定它不是极地情节。

在极坐标图中，绘图上的每个点也由两个值定位，但在这种情况下，它们是半径（距原点的距离）和半径与任意起始线之间的角度。这里，半径代表’确定性’，垂直角度代表’时间’。在这个视图中，我们看到随着时间的增加（当我们围绕图顺时针移动时），初始确定性（相同的50％）现在增加到最终值100％。也就是说，经过一段时间后，我们确定它是极地情节。

预期的笑话似乎是图表是确认偏见的练习。无论您最初假设哪种类型是正确的，该观点都将通过调查得到证实。这是因为两个不同的视图都是正确的 – 图表同样可以被认为是笛卡尔或极坐标图。这有点违反直觉。

在整个图中，两个概率的总和是100％，即（极坐标观察者确定图是极性的）+（笛卡尔观察者确定图是极性的）= 100％。图形的形状似乎是（以顺时针极性形式）r（t）= 100 /（1 + cos（t））。

如果读者心胸开阔，他们永远不会达到确定性（0％/100％取决于你如何阅读图表），因为没有足够的信息来明确决定这两种方式。

标题文本是一个笑话，如果你不确定如何标记任何双轴（二维）图形，你可以说它代表’作为时间的函数爬过我的屏幕的蚂蚁的坐标’，没有人然后可以与你的数据争论。 “嘿，那是他们走的路！”