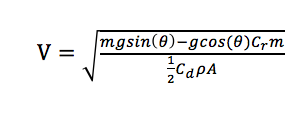假如把整塊美國大陸放在一個自西向東傾斜的斜坡上,那麼要多斜,我不用踩踏板,就能保持速度,騎著腳踏車從西邊滑到東邊去?
布蘭登如克斯
很可惜,這個坡太陡了,根本建不出來。不過至少你可以到夏威夷群島中的毛伊島度假。

根據物理學,腳踏車會往低處走。如果坡足夠長,腳踏車會達到一個穩定的滑行速度。在陡峭的坡上,這個滑行速度會很快;而在相對平緩的坡上,滑行速度則較慢。如果斜坡太平緩,腳踏車就會減速並停下。
腳踏車的滾動阻力係數決定了為了使腳踏車繼續向前滑行所需的最小坡度。事實上,計算這個最小斜率的公式簡單得不行,就是在水平距離上的高度落差:
最小斜率= 滾動阻力係數
在物理界,「斜率等於摩擦係數」[1]是一道非常好用的公式:一個物體與某一表面之間的摩擦係數正好等於這個物體開始向下滑動時的斜率 [2]。
一台普通腳踏車的滾動阻力係數可以低至0.002或是1/500 [3]。也就是說,如果你想要在水平距離上滑行個500英里,這個坡度至少要達到1英里。從洛杉磯到紐約2500英里的路程,你至少要從海平面5英里以上出發。這個高度比北美境內所有山還要高,我建議你攜帶氧氣罐。
溫馨提示:旅程費時較長,敬請耐心。
一台腳踏車的滾動阻力主要來源於輪胎在行進時的形狀變化[4][5][6],跟你的速度快慢並無太大關係。但是空氣阻力卻會隨著你的速度增快而增大。在大多數情況下,空氣阻力就是一台腳踏車最大的阻力。為了算出一台腳踏車能在斜坡上衝多快,我們就必須知道什麼時候空氣阻力能與重力在腳踏車前進方向上的分力相平衡,因為在那個時候腳踏車將會停止加速。我們可以利用空氣阻力公式進行計算:
重力在前進方向上的分力 = 滾動阻力+空氣阻力
mgsin(θ) = gcos(θ)Cr m + ½ρAV²Cd
(V是腳踏車速度,Cr 和Cd 分別是滾動阻力和空氣阻力,θ是斜坡角度,g是重力加速度,m是腳踏車和車手的質量,A是腳踏車和車手的迎風面積,ρ是空氣密度)
在一個僅有0.2或是0.3度的坡上,腳踏車基本不會移動,最高速度還不如走路快。斜坡還得更加陡峭些,才能使速度達到一個較為舒適的大小,但這就必須使洛杉磯的高度更加高於5英里了。
即便如此,腳踏車依然是十分出色的滑行器具[7]。而一般滑行能力較強的滑雪板,卻有著比腳踏車滾動阻力大10倍的摩擦係數。
如果你想從洛杉磯滑雪滑到紐約,這道滑雪坡至少得必腳踏車的斜坡高出10倍以上。所以你不能從山頂上出發,而得直接把宇宙當成你的起點啦。先不管這麼高的坡有沒有可能建出來,在外太空的低溫環境下,連冰都不一定能保持穩定。所以你根本是滑無可滑。
實際上,在極度理想的強況下,你能用腳踏車滑行最遠的距離大概不超過幾百英里。在現實世界裡,你能參加最長的旅程大概[8]就是哈萊亞卡拉山坡單車行了。在這趟旅程中,你無須出力,便可從將近10000英尺高的山峰飛車直騎35英里,直達夏日炎炎的海灘。

(如果你無法抽空前往毛伊島,至少看一看腳踏車騎到水裡的影片。)
註釋
[1] 滑動摩擦力和滾動阻力的原理並不一樣,但是在這類問題中,它們的係數是同等的。如果你想精確一點,你可以把它們都叫做「阻力係數」,但是「摩擦係數」更常用。 [2] 靜摩擦係數就是使物體開始滑動的坡度。如果你推動了物體,(通常數值較低的)動摩擦係數則是使該物體持續滑動的最小坡度。 [3] 請自行查考數據 [4] 同時與地面也有關係,你應該不想在泥土上滑吧 [5] 當然如果你的腳踏車是用黏土做的,輻條和框架也要考慮進去 [6] 不過誰會騎一台黏土捏的腳踏車啊 [7] 火車的鐵輪配有專門的鐵道,所以滾動阻力很小。你可以通過查閱數據來求出滾動阻力,但是聰明的你也可以看一看大力士拉動火車的影片。這樣,只要稍微計算一下人類力量的極限,或是直接測量,你就能算出另一側的係數了。結果火車車廂,或者說大力士比賽中常用的那些車廂,它們的滾動阻力跟一台單車相差無幾。 [8] 據說這是最長的。但是我一直很懷疑在蒙古野外還是哪裡會不會有那種天然的斜坡比它還長。