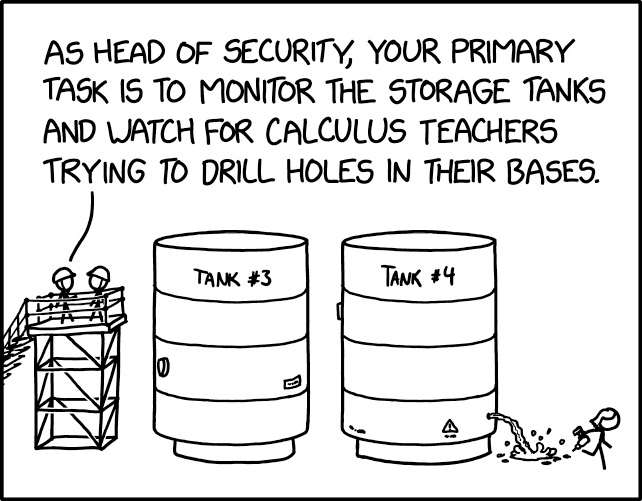
Title Text:We’re considering installing a pressurization system to keep the tanks at constant pressure solely to deter them.

Origin:https://xkcd.com/2974/

https://www.explainxkcd.com/wiki/index.php/2974:_Storage_Tanks

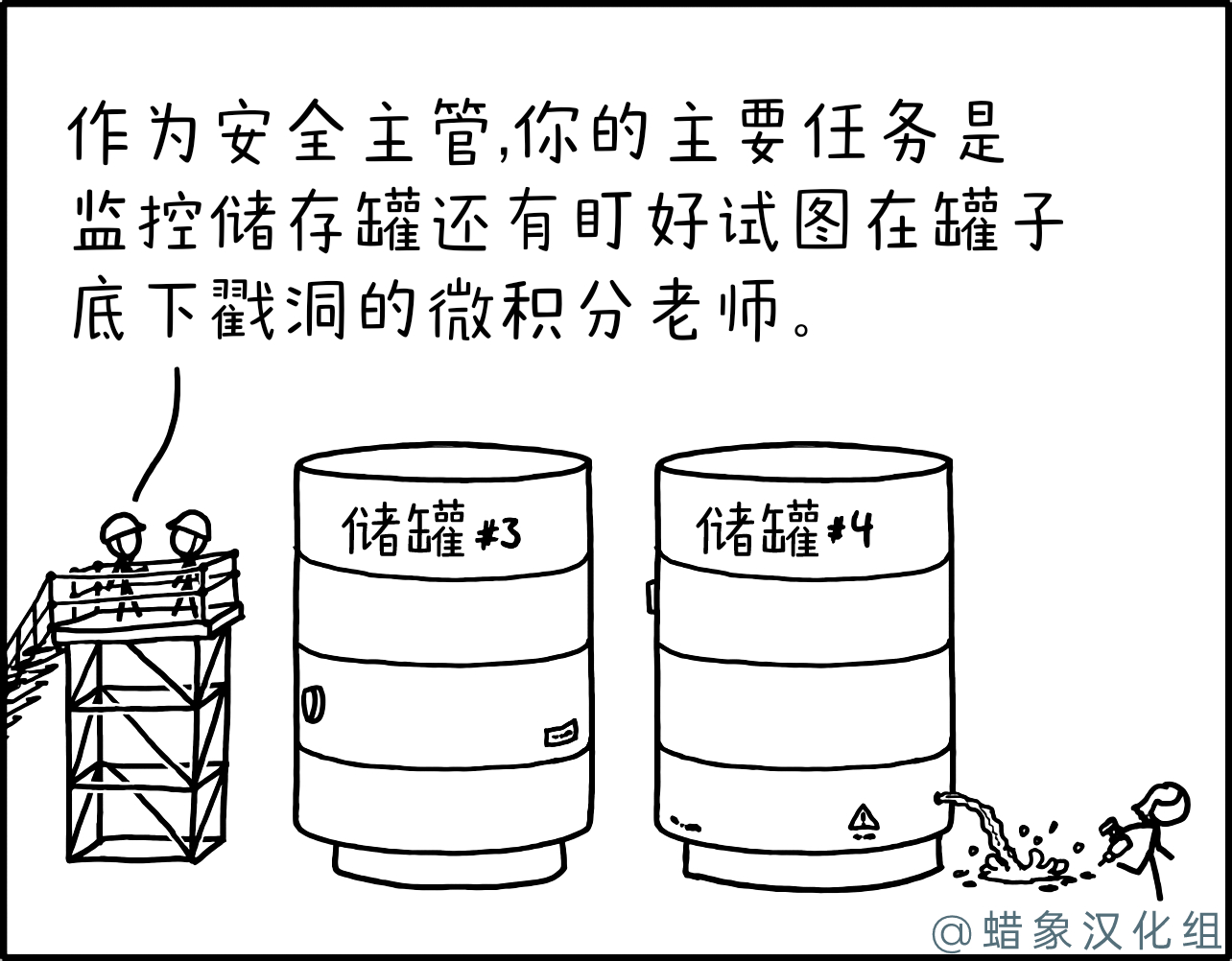
储存罐

https://xkcd.in/comic?lg=cn&id=2974

微积分是数学的一个分支，处理的是持续变化的值。为了展示这类数学的应用，初级课程通常会使用物理示例来说明方程如何在现实生活中应用。一个常见的问题示例是假设一个装满液体的水箱，底部有一个孔，让学生计算水箱排空的时间（通常假设为一个圆柱形水箱，顶部处于大气压下，从一个圆形孔中泄漏低粘度的液体，如常温下的水。）重要的变量有三个：水箱的半径、孔上方液体的高度和孔的大小。

在这种情况下，液位的变化是通过孔的流速的函数，而流速又是孔入口处液体压力的函数（根据托里切利定律），而那种压力又是剩余液体的高度的函数。因此，孔上方水箱中剩余液体的量将遵循二次衰减，这是微积分课程中涉及的一个概念。掌握微积分基础原理的学生应该能够计算水箱液位的下降。更高级的版本的问题可能涉及(A) 一个水箱排水到第二个水箱，然后排到地面，或(B) 一个密封的水箱，其中液体下降时顶部的空气压力下降。

如前所述，许多STEM教师喜欢使用现实世界的例子，理想情况下进行物理演示，以使抽象概念更加难忘。教师可能会用水填满一个水壶，在侧面打开一个孔，并邀请学生将观察到的流出速率与他们的计算进行比较。这幅漫画暗示薇薇安·伦哈特小姐将这个主意推向了极端，她进入了一个工业现场，在一个大型充满液体的桶上钻了一个孔。可以想象，她的班级要么远远观看，要么以某种方式拍摄漏水的过程。

戴安全帽的员工之间的对话暗示有一阵微积分教师进行类似的演示，以至于安保负责人主要的工作是防止这种教学动机导致的破坏。在现实生活中，这种破坏是严重的，因为会有因受损的桶、加压液体或危险物质带来的安全风险（注意桶上的警告标志）。

标题文字开玩笑地提到，保持在漏水处的恒定压力，流速也将变得恒定，因此液位的下降将是线性的，从而大大简化了这个问题，消除了微积分的需求。这个更简单版本的问题可能会阻止微积分教师将其用作演示——尽管它可能会吸引同样大胆的代数教师。

分析与计算[编辑] 漫画观察表明以下假设：

孔上方水箱高度：约20英尺
水箱半径：约6英尺
钻头类型：普通螺旋钻（非孔锯）
钻头尺寸：1英寸（市面上最大常见螺旋钻头）
伦哈特小姐的目标：向她的学生展示二次衰减
考虑一个20英尺高、6英尺半径且带有1英寸直径钻孔的水箱，完全排空大约需要21.5小时——时间太长，不适用于课堂演示——但是也许可以拍摄成延时视频？——尽管可能会由附近的工人水平上修复这个泄漏。
要在36分钟内排空水箱，需要一个6英寸直径的孔。
因此，钻头的大小、喷涌的液体流和这个现实世界示范的可行性之间显然存在不匹配。液体的粘度和密度也是一个未知因素；为了便于计算，微积分问题通常假设液体是普通水（根据定义，其密度为1.00*（1公斤/升（8.35磅/加仑））和粘度为1.001微帕斯卡）或主要由水组成的混合物（具体取决于它还包含什么，如溶解固体或其他物质）。

一个解释是，她能够在短时间内钻出几十个约1英寸的孔，而有毒液体正在喷涌而出，但钻头似乎并没有滴水。
但最可能的解释是，兰德尔没有考虑钻孔和钻头大小与明显的孔大小之间的关系，只有漫画解释网站的挑剔编辑才会注意到并关心这个问题。
或者，水箱在老师钻孔的时候根本没有满。