Title Text:PERPETUALLY OPTIMISTIC CASE: Early in the execution, our research group makes a breakthrough in proving P=NP.

Origin:https://xkcd.com/2939/

https://www.explainxkcd.com/wiki/index.php/2939:_Complexity_Analysis

复杂度分析

https://xkcd.in/comic?lg=cn&id=2939

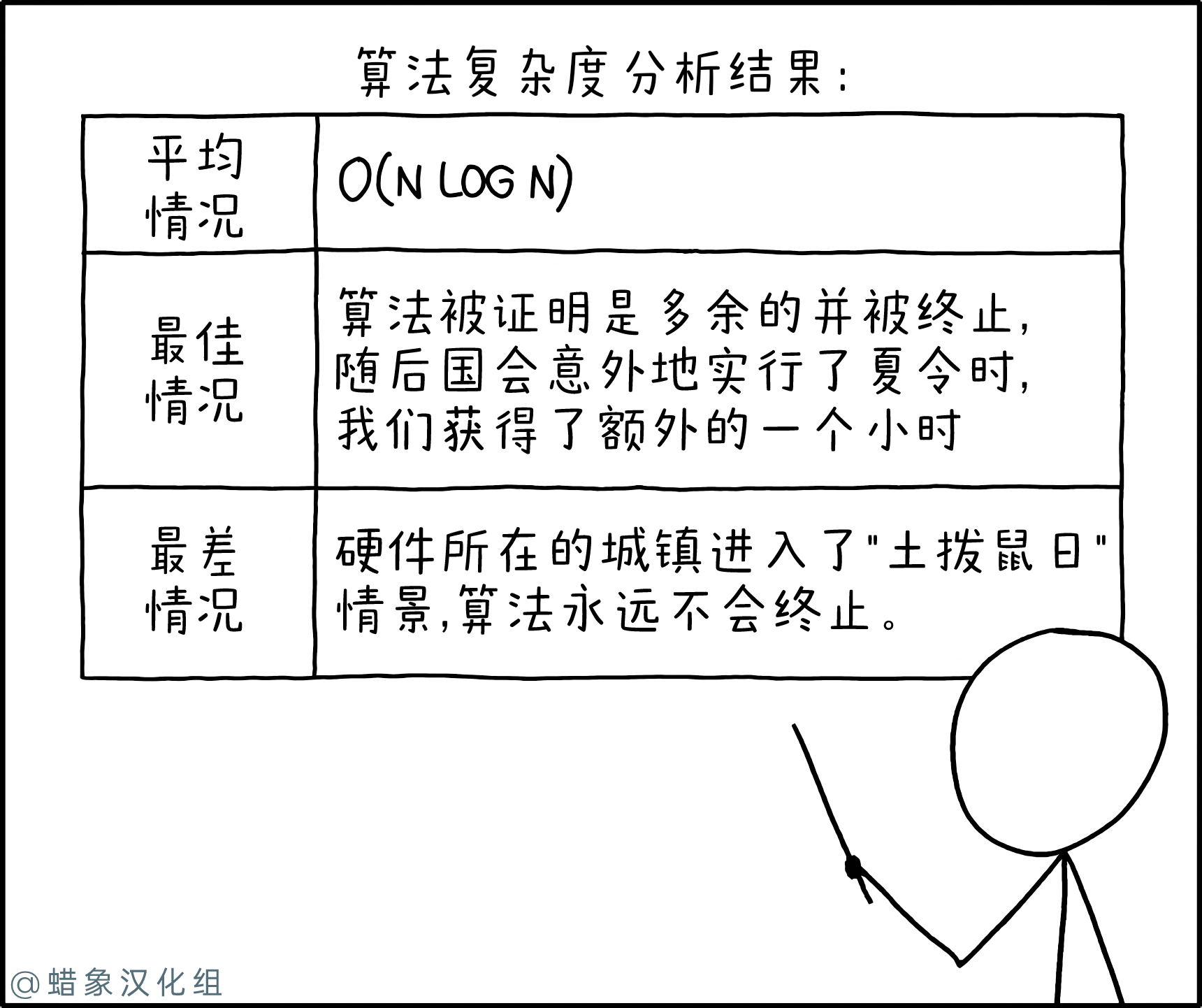
Cueball正在讲解一个算法的复杂性。该算法的平均情况复杂性用大O符号表示为O(n log n)，表达了随着输入数量不断增加，算法的渐进运行时间。
漫画的笑话在于将“最佳情况”和“最坏情况”的术语比原本意图的理解得更为宽泛和字面。Cueball不仅提出了函数输入数据的最佳/最坏情况，还考虑了整个全球环境，包含诸如美国国会这样显然超出算法范畴的因素。
特别是，这个笑话涉及对一个封闭系统的分析，这在工程学中很常见。一个算法的“最佳情况”通常是当其输入具有最佳值时的运行时间，并且耗时尽可能少。其中一个例子是，当调用一个已经排序的数字列表时的排序算法；在这种情况下，算法只需在一次遍历中检查列表中的每个项目以确认已排序，相比之下，须在多个周期中将任意数量的项目与任意数量的其他项目进行比较。最坏情况则是当列表以某种方式呈现出最大数量的挑战和操作给排序算法时（可能是，且不一定，是以完全错误/反向的顺序呈现的初始列表）。这两个极限都可以用O-符号表示，但单个O-符号通常表示所有输入中遇到的平均操作复杂性。
这里的笑话在于，虽然该算法被提早终止，因为被认为是“没有必要”，从而“运行”得比原本被认为的最佳情况更快，但其运行时间似乎还因为国会的一项行动改变了夏令时，减少了一个小时，返回的结束时间（按当地时间）比在其他情况下要少一个小时。这可能导致结束时间记录为早于开始时间（取决于如何处理时间），因此产生明显的负“运行时间”。夏令时是xkcd中的一个反复出现的主题，很明显Randall对此并不感冒，因此国会作出的意外夏令时更改是Randall嘲讽这一概念的又一种方式。
“最坏情况”指的是电影《土拨鼠日》，其中相同的事件一遍又一遍地发生在某种时间循环中。（这部电影在1076：土拨鼠日中曾被提及。）如果运行算法的硬件存在于这种循环中，那么它也可能在完成之前重置到之前的时间，这意味着算法将永远不会终止。这引发了一个关于电影的哲学问题，即整个世界是否在每一天之后重置，还是仅仅是故事发生的城镇。如果只是这个城镇，并且你仍然可以从外部连接他们的硬件，那么从这个角度来看，算法似乎耗费了无尽的时间来运行。如果整个世界重置，由于人们（除了电影的主角）没有经历重置，因此必须等到最后一次（不重置的循环）导致进入预期的下一天，才会显得时间如此之长。
这可能间接提到停机问题，这是计算机科学中的一个著名问题。停机问题是不可判定的，这意味着没有通用算法能够判断一个给定的算法是否会停机，但广泛接受的传统证明依赖于对被视为封闭系统的细节进行外部操作。
标题文字可能提到计算机科学中甚至更加著名的问题：P与NP。这是询问每个其解决方案可以快速验证（在非确定性多项式时间内，NP）的基本问题是否也可以快速解决（在多项式时间内，P）。P与NP问题是七个千年奖问题之一，因此有100万美元的奖金作为解决方案。可以推测，这里讨论的问题是在NP中，因此如果P=NP，其最坏情况下的运行时间将是某个多项式O(nk)。然而，P与NP问题之所以成为千年奖问题是有原因的；大多数计算机科学家预期P≠NP，因此希望在证明P=NP方面取得突破是“永远的乐观”。这可能是对乐观偏差和规划谬误的引用，即人们倾向于假设最有利的结果是最可能发生的。