Title Text:So what do we do when we get to base 10? Do we use A, B, C, etc? No: Numbers larger than about 3.6 million are simply illegal.

Origin:https://xkcd.com/2835/

https://www.explainxkcd.com/wiki/index.php/2835:_Factorial_Numbers

阶乘进制数

https://xkcd.in/comic?lg=cn&id=2835

阶乘是正整数的乘积。例如，四的阶乘，写作’4!’，表示4脳3脳2脳1=24。
数字系统的“基数”定义了它使用哪些数字作为数字，以及数字中每个位置的值意味着什么。例如，在十进制数字（基数10）中，数字从0到9，位置值是个位、十位、百位等等。因此，“137”表示1脳100 + 3脳10 + 7脳1 = 137。数字也可以用其他基数表示，比如二进制（基数2，使用数字0和1，位置值为1、2、4、8…）或八进制（基数8，使用数字0-7和位置值为1、8、64，依此类推）。使用不同的基数并不常见，但在计算机科学中有时是有用的。
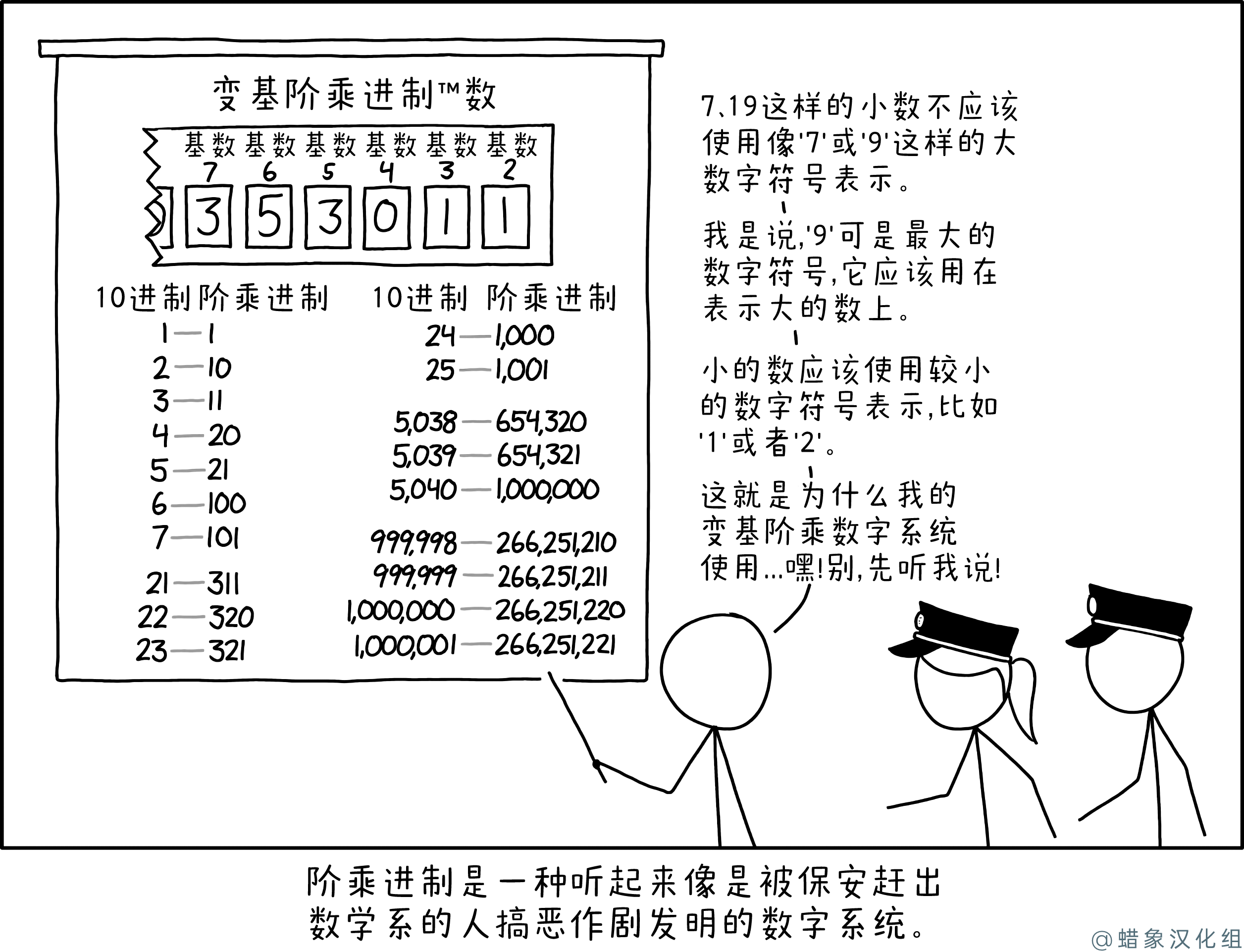
在漫画中，Cueball 提出了一个阶乘数字系统，其中每个位置值的基数不同——第一个数字可以是0或1，下一个数字可以是0、1或2，第三个可以是0、1、2或3，依此类推。每个位置值是基数的阶乘。因此，十进制的数字137可以写作10221，表示1脳5! + 0脳4! + 2脳3! + 2脳2! + 1脳1!。虽然这个数字系统在技术上是可用的，并且可以表示任何数字，但似乎过于复杂，Cueball 认为使用它的唯一原因是他认为像9这样大的数字只应该在巨大数字中使用（9只有在数字至少9位长或在十进制中超过320万时才会使用）。这是使用一个新数字系统的荒谬理由，[引用需要] 所以数学系认为这是一个恶作剧，保安把他赶了出去。
在标题文本中，有人指出阶乘数字系统每个位置值需要越来越多的数字。在阶乘数字中，第十个数字将在基数11中，这需要11个可能的数字，而0-9仅提供10个。在高于10的基数中，可以使用字母表示更高的数字。例如，十六进制（基数16）从0到9，然后从A到F。对于阶乘数字中的更高基数，采用相同的方法是合理的。相反，Cueball 说写大于约360万的数字是非法的，这是使用基数不超过10的最大限制。这是一个荒谬的限制，因为其他数字系统可以按你喜欢的方式增长。
Cueball 演示文稿顶部的数字353011是3脳6! + 5脳5! + 3脳4! + 0脳3! + 1脳2! + 1脳1!，其十进制值为2835，即漫画的编号。
Cueball 在因式分解中写的数字示例在OEIS中出现为序列A007623。