Title Text:I also managed to improve the solution for n=1 to s<0.97, and with some upgrades I think I can hit 0.96.

Origin:https://xkcd.com/2740/

https://www.explainxkcd.com/wiki/index.php/2740:_Square_Packing

方形堆积方案

http://xkcd.in/comic?lg=cn&id=2740

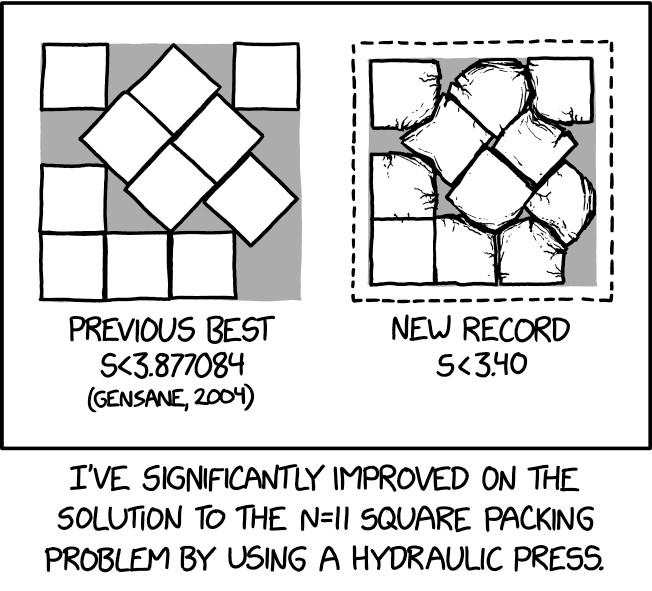
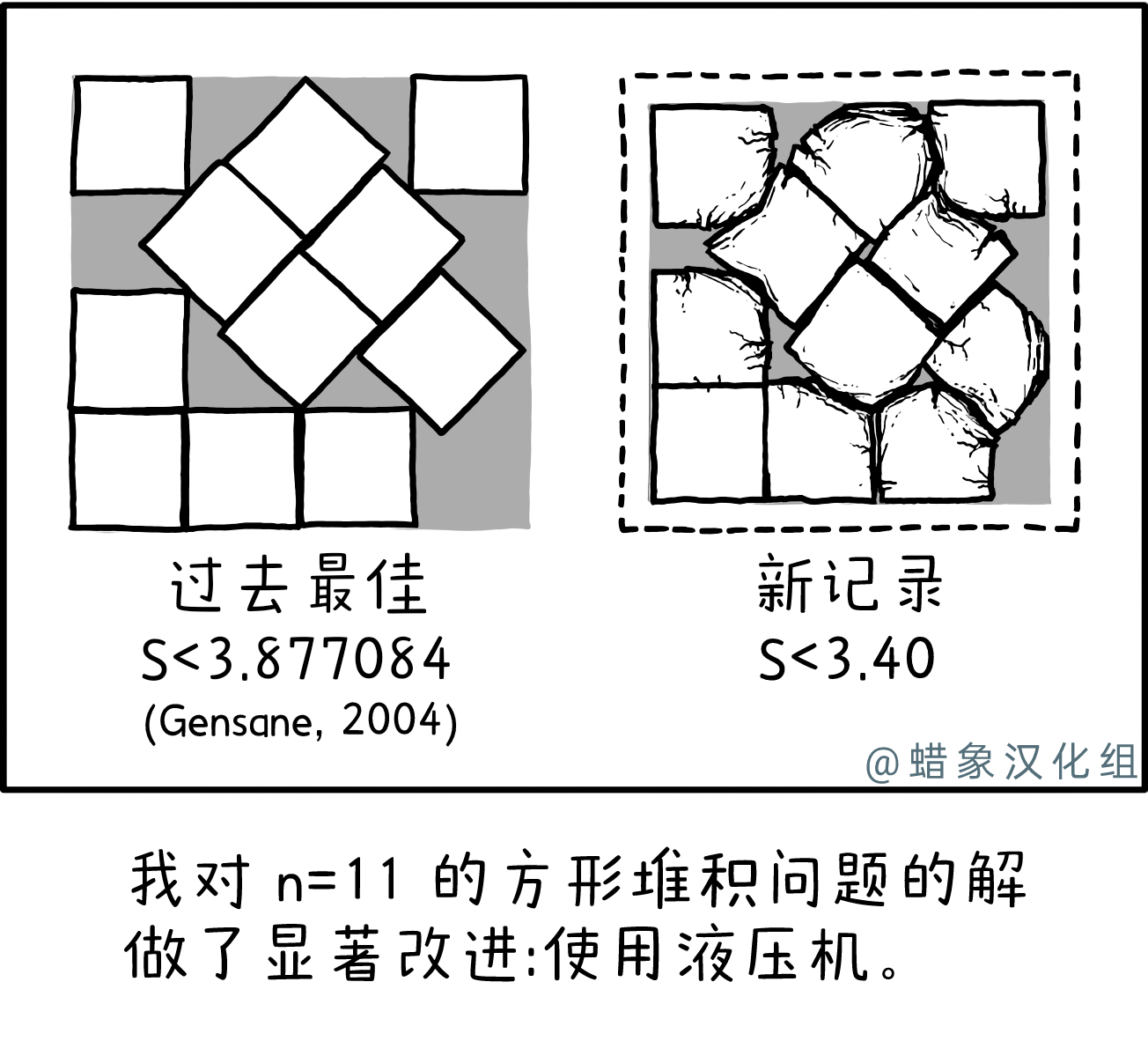
方形装箱问题是一种几何问题。目标是找到最小的可能适应N个”内方块”的”外方块”，每个内方块都是1个单位宽和1个单位高。在这个漫画中N=11，因此被称为”N=11方形装箱问题”，并且’value=’s’是外方块边长的长度。 （例如，用16个方块排列成4×4的方形，’s’将为4。[这里插入一张图片将会有帮助]）
这个漫画嘲笑了一些N值的常见现象：有时候最优解看起来在人类的感觉中非常”凌乱”。缺乏统一的网格或模式，导致一些方块看起来错位或者有很多空间被浪费，出人意料地导致了比更”有组织”的解决方案更小的’s’值。 ‘N=11’是这样一个”令人沮丧”的解决方案（尽管应该注意到，所描绘的解决方案尚未被证明是最优的）。
在这个漫画发布几天前，一个名为”Squares in squares”的网页在Twitter和Hacker News等社交媒体平台上引起了关注。对于许多N值，该页面描绘了已知的最佳解决方案，其中一些已知是最优的。对于N=11（已知最佳但尚未证明是最优的），这是Randall在这个漫画中使用的解决方案；它的一般排列是由沃尔特·特朗普在1979年发现，并由Gensane等人在2004年稍作改进。
Munroe声称已经找到了一个在这种N=11情况下更高效的解决方案，即通过用液压压力机对已知最佳解决方案中涉及的方块进行物理变形。得到的外接方块的尺寸确实更小，但这个”解决方案”实际上并不是一个解决方案，因为内部形状有无数皱纹，不再是方块。在装箱问题中，几何形状通常不被假设可以以这种方式变形。[需要引证] 标题文本提到了同样的方法”改进”了单位方块的解决方案，其最优解显然是单位方块本身，s=1。Munroe指出，如果他有”一些升级”，可能是一个更强大的液压压力机，他可以使得得到的方块甚至更小。
这个漫画和标题文本的幽默含义是，与其说这些形状是数学的、抽象的形状，不如说它们实际上是由一些极强但不完全不可压缩的材料构成的物理方块。这种材料可能不明显：即使使用液压压力机，其横截面积也只能缩小到原始尺寸的92-94%。（理论上的方块存在于问题陈述中的二维宇宙中，但这里看起来是三维物体，通过液压压力机从上方和侧面依次挤压后，显示出所朝向观察者的侧面的变形，这个问题没有更全面地解决。）
这可能是与2706号笑话有关，但现在是通过方形和压缩区域而不是三角形和延伸长度。未解决的装箱问题似乎也是Randall长期以来的兴趣，他在”What If？Expensive Shoebox”中展示了他思考”尺寸统一的圆形切割钻石的最高效装箱”，标题文本是”一次未解+装箱+问题的谷歌搜索差点让我悔过”。

引用：
[1] Gensane, T., Ryckelynck, P. “Improved dense packings of congruent squares in a square. Discrete Comput Geom 34, pages 97-109 (2005). https://doi.org/10.1007/s00454-004-1129-z