Title Text:3D graphs that don’t contact the plane in the closure area may proceed as scheduled, but be alert for possible collisions with 2D graph lines that reach the hole and unexpectedly enter 3D space.
Origin:https://xkcd.com/2735/
https://www.explainxkcd.com/wiki/index.php/2735:_Coordinate_Plane_Closure
平面直角坐标系封闭
http://xkcd.in/comic?lg=cn&id=2735
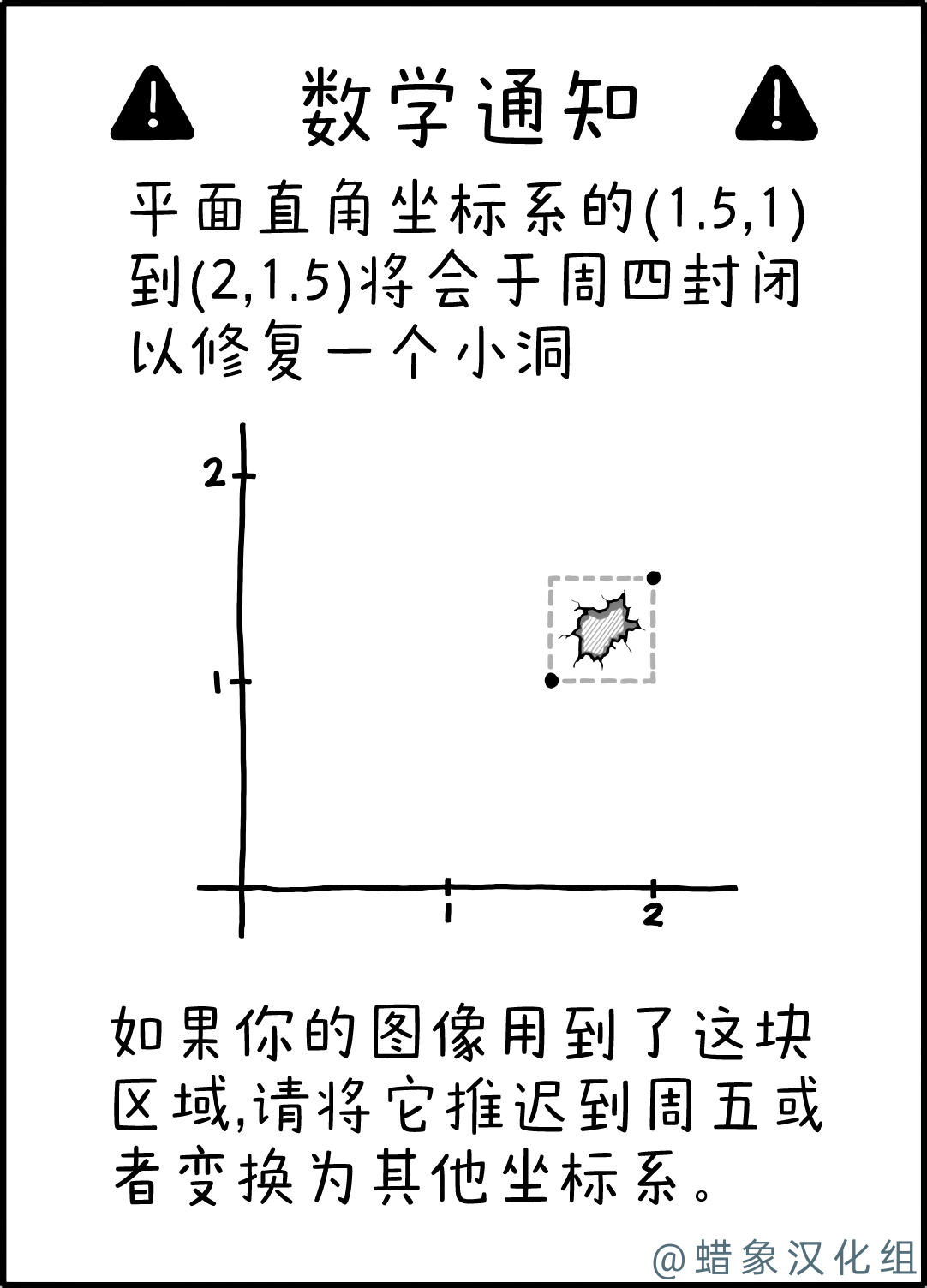
这本漫画是一则“数学公告”,可以假设是为数学家或其他与数学领域有交集的人提出的警告或提醒,类似于“旅行公告”可以预先警告驾驶员计划中的道路封闭修复(或火箭发射)。它也类似于航海通告或航空任务通告,其中海上或航空导航可能会受到即将到来需要保持清空的区域(或体积)的影响,以及网站或软件提供商关于计划维护的通知,提醒用户即将发生的中断。具体而言,该公告建议那些使用坐标平面的人在有洞的区域里避免绘制任何图形,直到损坏得到修补或修复。
这个笑话可能是作为对2023年中国气球事件的回应而产生的,事件发生在几天前。这引发了美国历史上最大范围的临时飞行限制,对此作出了关闭领空的回应。
在数学中,坐标平面用于绘制图形。这个笑话的意思是一个小部分被“关闭以进行维护”,将坐标平面的概念比作数学中实际使用的一个物理平台,因此容易受到像漫画中展示的损坏等破坏。实际上,坐标平面无法受损,因为它不是一个有形的物体。[需要引证]
在数学中,闭包可以是涉及集合的术语,特别是集合上的运算,而坐标平面是一组特定的数。如果一个集合在运算下包含所有的“答案”,则称该集合在该运算下是闭合的。例如,坐标平面可以说是对向量加法是闭合的 – 将任意两个坐标相加会产生另一个坐标在平面中。许多函数和运算符可以说在实平面上具有闭合性,这个漫画可能是对该术语的双关语。然而,如果平面上确实有洞,那么平面将不再具有闭合性。
与闭包相关的还有闭包问题。简单地说,闭包问题是在某种类型的图中找到闭包的最高或最低权重。这个漫画可能也在谈论闭包问题,因为它谈论了图中的洞,并且要将其最小化将涉及到闭包问题。
闭包还可以用于另一种意义上,与集合的拓扑有关;粗略地说,描述了集合的哪些部分“靠近”其他部分。在这个意义上,如果对一个带有洞的平面取闭包,结果确实是一个完整的平面,前提是洞足够(无穷小)小。
标题文字指出,穿越相关的x和y坐标的3D图形,但在该区域内,z坐标非零的情况下,应该是可以的,因为洞只存在于z=0的平面上。然而,如果它们接近-即在该区域内z坐标很小-他们应该警惕二维图形线突然变成三维并对其产生干扰。这可能是因为它们故意进入三维空间以避免闭合,或者可能是它们被撕裂和变形的表面边缘“发射”到平面上方/下方。或者它们只是掉进了洞中,从而进入三维空间。这类似于对开放车道中的道路交通发出警告,提醒他们有来自由于工程施工而关闭的车道并入的交通流量,或者对用作绕行道路的平行路线上的交通量增加的一般警告。
二维物体突然进入三维空间的概念-以一种产生有趣戏剧冲突的方式-是一本书《平面国》的主题,兰德尔对此很熟悉,因为这是721: 平面国的主题。




