Title Text:My liege, we were able to follow the ship into Minkowski space, but now they’ve jumped to Hilbert space and they could honestly be anywhere.
Origin:https://xkcd.com/2646/
https://www.explainxkcd.com/wiki/index.php/2646:_Minkowski_Space
闵可夫斯基空间
注释:
闵可夫斯基空间:在数学物理学中是指由三维欧几里德空间与时间组成的四维流形,其中任意两个事件之间的时空间隔与所依照的惯性系无关。尽管赫尔曼·闵可夫斯基一开始是为了电磁理论的麦克斯韦方程组而发展这一理论,但闵可夫斯基时空的结构却可以从狭义相对论的公设直接推出。
希尔伯特空间:在数学里,希尔伯特空间即完备的内积空间,也就是一个带有内积的完备向量空间。希尔伯特空间是有限维欧几里得空间的一个推广,使之不局限于实数的情形和有限的维数,但又不失完备性(而不像一般的非欧几里得空间那样破坏了完备性)。
http://xkcd.in/comic?lg=cn&id=2646
比光速旅行更快,在我们的宇宙中是不可能的,在科幻小说中经常被描述为让宇宙飞船进入(或“跳跃”)到一些不同的领域,称为“超空间”或类似的技术问题,在那里超光速旅行可以在返回平凡之前发生宇宙。在这部漫画中,一艘宇宙飞船被一艘敌舰追赶,船员们试图通过跳入Minkowski 空间来逃跑,该空间实际上只是传统的 3-D 空间,与时间结合成一个数学对象,称为狭义相对论中使用的流形。因为闵可夫斯基空间只是真实物理时空的表示,“跳”进去是没有意义的,对逃避追捕没有任何好处,提供了漫画荒谬笑话的幽默感。
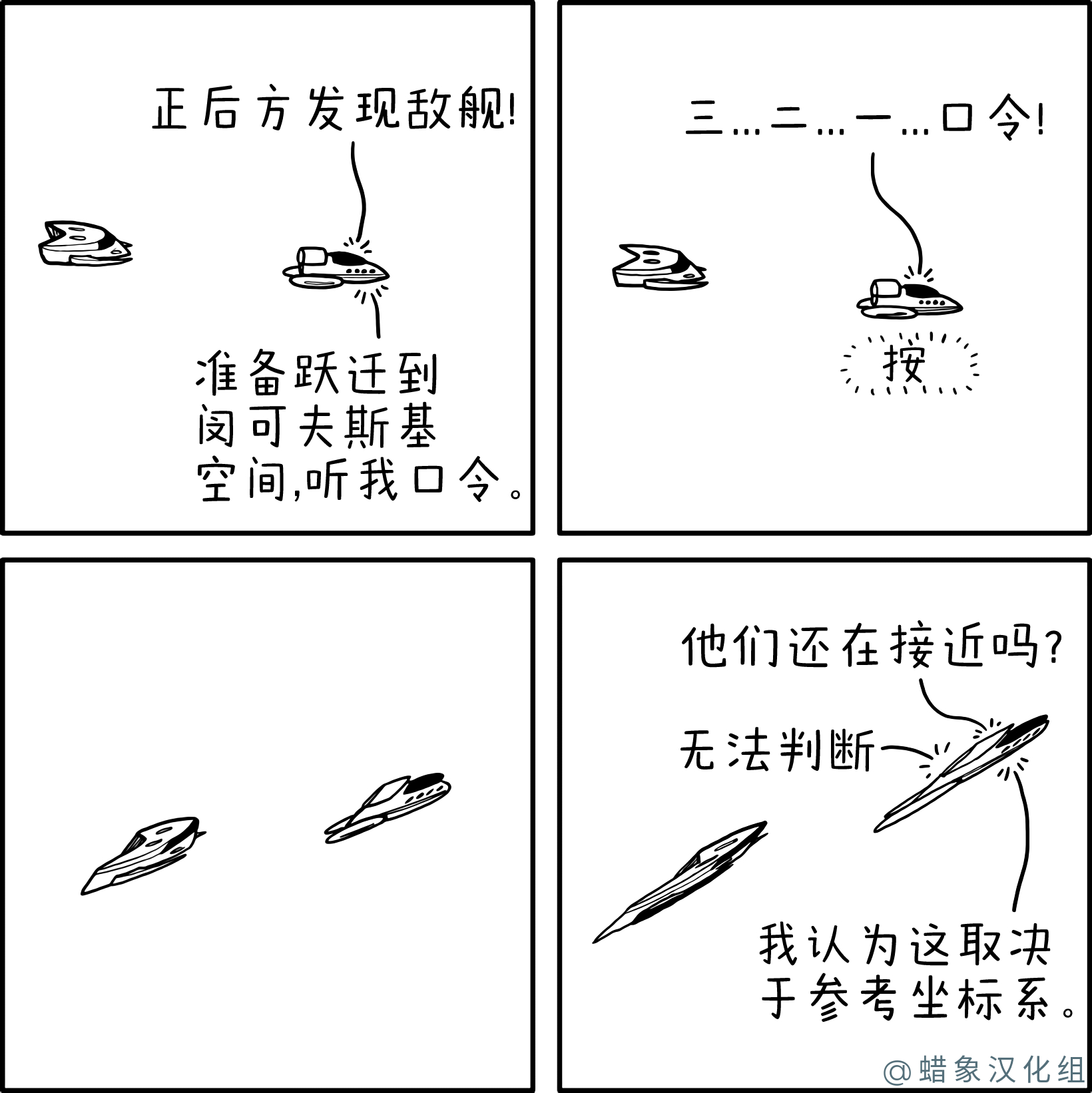
对角倾斜的宇宙飞船的视觉描绘是基于闵可夫斯基空间中物体的图形闵可夫斯基图表示,其中物质的世界线被限定在其对角光锥内。
提到的距离取决于观察者的参考系,是指在不同的惯性参考系中测量时距离的变化,这个概念称为同时性的相对性。以下是一些旨在解释该概念的视频。所描绘的倾斜改变了飞船之间的距离,使得追赶者的尖端更靠近被追赶的飞船,但它们的中心更远。因此,对于漫画的读者来说,他们是否更接近了这个问题是不确定的。[需要引用]
标题文本是追击飞船中某人向他们的领导(他们称之为“我的领主”)的状态报告。跟随飞船到 Minkowski 空间不是问题,但被追捕的飞船随后跳到了 Hilbert 空间,现在可以任何地方。隐藏在希尔伯特空间更容易,因为希尔伯特空间(其中有许多非常不同的变体,不像闵可夫斯基空间)可以有无限维数,因此比四维闵可夫斯基时空复杂得多。然而,希尔伯特空间是一种数学结构,用于描述各种参数和复杂度的函数等对象,而不是物理时空现实,因此在希尔伯特空间中表示物理对象是非常不寻常的。量子态可以表示为希尔伯特空间中的向量,因此它可能与关于逃逸宇宙飞船如何在任何地方 的不确定性原理有关。
和《追海》漫画一样,跳到这里的空间也不止一种。




