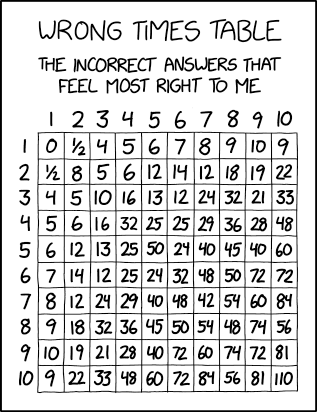
Title Text:Deep in some corner of my heart, I suspect that real times tables are wrong about 6×7=42 and 8×7=56.
Origin:https://xkcd.com/2313/
https://www.explainxkcd.com/wiki/index.php/2313:_Wrong_Times_Table
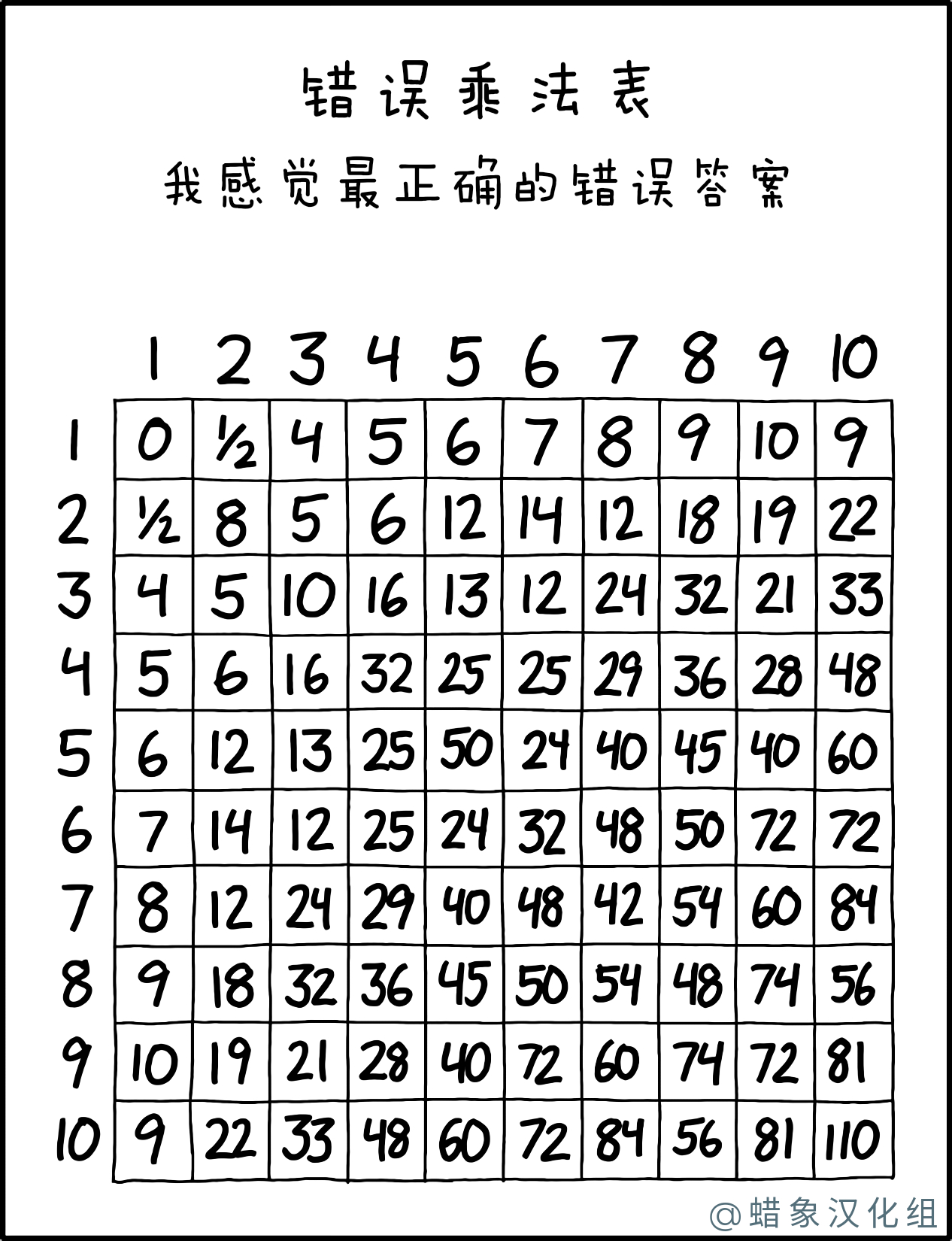
错误乘法表
脚注:
[1]42:科幻小说《银河系漫游指南》中的梗,生命、宇宙和一切的终极答案都是42。作者后来承认这就是拍脑袋随意编的。
http://xkcd.in/comic?lg=cn&id=2313
“时间表”(或乘法表)是用于显示数字乘积的表。通常,小学生被要求记住最多10个整数的表,作为学习算术的一部分。
在这个漫画兰德尔提供他自己的乘法表的替代版本,具有完全不正确的值,但“感觉”对他来说是正确的。尚不清楚他的值是如何得出的,因为它们的值并不遵循一致的模式,但可能是在计算产品时,他有时不得不更正其心算,也许是按照“ 8 * 4是36”的思路思考。 ..或者,等等,是32岁吗?”。大多数值从其正确位置进行转置(例如,从一个或两个被乘数中加或减一个或两个或三个),有些值“偏离一”(或二或二) ),则可以通过将两个因子相加,相减或相除而不是相乘来创建一些(主要在1行和1列中)。值得注意的是,某些数学性质没有得到遵守,
该表是对称的,表明Randall的乘法形式是可交换的。
标题文字(指的是Randall怀疑6×7 = 42可能是错误的)是对《旅行者》银河指南的暗示,其中对生命,宇宙和一切的终极答案据说是四十二。但是,在书中,如果不知道最终问题,这个答案就毫无意义。,因此为了计算最终问题,构建了一个行星大小的计算机。后来变成了地球,但是地球在完成计算之前不久就被破坏了。亚瑟·登特(Arthur Dent)是最后幸存的人类之一,有一些白色老鼠(对我们来说像白色老鼠的超维生物)试图让他把大脑给他们,所以他们可以尝试重现最终的问题,希望可能是自从他成为计算机矩阵的一部分以来,它一直存储在他的大脑中,直到地球被毁坏前几天才完成一千万年的计算。亚瑟拒绝了,老鼠们试图思考一个使答案42有意义的问题,例如“ 一个人必须走多少路“。他们还提出了6×7的建议。亚瑟(Arthur)稍后尝试通过从书包中挑选字母拼写自己来重现问题,并产生一句“如果将六乘以九会得到什么?”。这使他评论道:“我一直想着根本上错了宇宙。”但是请注意,该行星计算机的运行已中断,因此宇宙也可以正常运行,并且只计算了错误的问题。发生时,以13为底的6×9 = 42但是道格拉斯·亚当斯(Douglas Adams)否认这仅仅是巧合,在Randall的表中,没有说6×7和6×9的结果是42,而7×7的结果是42。
如果我们将较小的被乘数视为a,将较大的被乘数视为b,则Randall使用的公式(的无穷多个可能性之一)如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | a-b | a/b | a+b | a+b | a+b | a+b | a+b | a+b | a+b | b-a |
| 2 | a/b | 2ab | a+b | a(b-1) | a(b+1) | a(b+1) | a(b-1) | b+10 | b+10 | a(b+1) |
| 3 | a+b | a+b | ab+1 | (a+1)b | a(b-1)+1 | (a-1)b | a(b+1) | (a+1)b | a(b-2) | a(b+1) |
| 4 | a+b | a(b-1) | (a+1)b | 2ab | (a+1)b | (a+1)(b-1) | ab+1 | a(b+1) | a(b-2) | a(b+2) |
| 5 | a+b | a(b+1) | a(b-1)+1 | (a+1)b | 2ab | (a-1)b | a(b+1) | a(b+1) | a(b-1) | (a+1)b |
| 6 | a+b | a(b+1) | (a-1)b | (a+1)(b-1) | (a-1)b | (a-2)(b+2) | a(b+1) | ab+2 | a(b+3) | a(b+2) |
| 7 | a+b | a(b-1) | a(b+1) | ab+1 | a(b+1) | a(b+1) | a(b-1) | (a-1)(b+1) | (a-1)(b+1) | a(b+2) |
| 8 | a+b | b+10 | (a+1)b | a(b+1) | a(b+1) | ab+2 | (a-1)(b+1) | a(b-2) | ab+2 | a(b-3) |
| 9 | a+b | b+10 | a(b-2) | a(b-2) | a(b-1) | a(b+3) | (a-1)(b+1) | ab+2 | a(b-1) | a(b-1) |
| 10 | b-a | a(b+1) | a(b+1) | a(b+2) | (a+1)b | a(b+2) | a(b+2) | a(b-3) | a(b-1) | a(b+1) |